Customized Importance Sampling Using User-Defined Realization Weights

For risk analyses, it is often necessary to evaluate the low-probability, high-consequence portions of the probability distribution A mathematical representation of the relative likelihood of a variable having certain specific values. It can be expressed as a PDF (or a PMF for discrete variables), CDF or CCDF. of the performance of the system, and that can require carrying out a very large number of Monte Carlo realizations. Because the models for such systems are often complex (and hence need significant computer time to simulate), it can be difficult to use the conventional Monte Carlo for such risk analyses.

To facilitate this type of analysis, GoldSim allows you to utilize an importance sampling An algorithm that biases sampling of probability distributions in order to better resolve the tails of the distributions. algorithm to modify the conventional Monte Carlo approach so that selected portions of input distributions (which could correspond to high-consequence, low-probability outcomes) are sampled with an enhanced frequency. During the analysis of the results that are generated, the biasing effects of the importance sampling are reversed. The result is high-resolution development of "high-consequence, low-probability outcomes", without paying a high computational price.

Stochastic elements provide built-in functionality to force importance sampling on either the low end or high end of a Stochastic element An element that can be used to quantitatively represent the uncertainty in a model input.'s range (i.e., the tails of distribution). Timed Event An element that generates discrete event signals based on a specified rate of occurrence. and Random Choice elements provide similar functionality.

In some cases, however, it may be necessary apply importance sampling not just over the tails, but over user-defined regions of the Stochastic element's range. For example, if it was known that the important results of a model were highly sensitive to values of a particular Stochastic that were close to the 40^th percentile, you would want to focus sampling in that region.

GoldSim supports this by providing three specialized functions that provide biased sampling (and compute the appropriate weights) for a targeted range within a probability distribution. All three functions require a Target probability and a Width. For example, if you specify a Target of 0.4 and a Width of 0.05, biased importance sampling will be focused in the region between probability level 0.375 and 0.425. The functions provided by GoldSim are as follows:

ImpProb(Old,Target,Width): Takes a sampled probability (Old) and returns a probability biased toward the specified region (the manner in which this is done is discussed below).

ImpWeight(Prob,Target,Width): Takes a biased probability (produced by ImpProb) and returns a weight.

ImpOld(Prob,Target,Width): Takes a biased probability (produced by ImpProb) and returns the unbiased probability. This is the inverse of ImpProb.

By using these functions in conjunction with GoldSim's option for the user to manually specify realization A single model run within a Monte Carlo simulation. It represents one possible path the system could follow through time. weights, a customized importance sampling scheme can be implemented.

The steps required to implement importance sampling on a single Stochastic element (e.g., named Stoch1) with a Target of 0.4 and a Width of 0.05 are as follows:

1. Create a Stochastic element (e.g., U) defined as a Uniform between 0 and 1. This will generate a random number.
2. Create an Expression element A function element that produces a single output by calculating user-specified mathematical expressions. (e.g., Prob) defined as "ImpProb(U,0.4,0.05)". This will generate biased random numbers with which to sample Stoch1.
3. Create an Expression element (e.g., Stoch1Value) with the same dimensions An output attribute for an element that defines the dimensionality (in terms of Length, Time and other fundamental dimensions) of the output. of Stoch1, defined as "PDF_Value(Stoch1.Distribution,Prob)". This will generate the biased sample of Stoch1.
4. Create an Expression element (e.g., Weight) defined as "ImpWeight(Prob,0.4,0.05)". This computes the appropriate weight to use for the realization.
5. Open the Simulation Settings dialog, and go to the Monte Carlo tab. In the Probabilistic Simulation A simulation in which the uncertainty in input parameters is explicitly represented by defining them as probability distributions. section, check the Specify Realization Weights box. An Insert link dialog will appear, and you should select the Weight element defined in the previous step. This then instructs GoldSim how to appropriately weight each realization when computing results (e.g., CDFs).

This specific example can be found in the file CustomImportance.gsm in the General Examples/Stochastic folder of your GoldSim directory (accessed by selecting File | Open Example... from the main menu).

How does GoldSim actually implement this importance sampling? The implementation is as follows:

During the Monte Carlo simulation A method for propagating (translating) uncertainties in model inputs into uncertainties in model results. half of all the random numbers generated by the importance sampling function (ImpProb) will lie outside of the enhanced-sampling region (defined as the region from Target - Width to Target + Width), and half inside it. The “outside” and “inside” regions are sampled differently:

• The half of the samples that are outside the region are distributed uniformly.
• The sampling of the half that are inside of the zone depends on whether the target probability is close to 0 or 1:
  • Normally, these samples have increased sampling rates closer to the target value. The sampling rate within the enhanced sampling zone is distributed according to a truncated normal distribution, with a standard deviation The square root of the variance of a distribution. The variance is the second moment of the distribution and reflects the amount of spread or dispersion in the distribution. equal to one quarter of the width of the zone.
  • However, if the target probability level is less than the specified width, or greater than (1 - the specified width), then the enhanced samples are also uniformly distributed, though sampled at a higher rate than the samples outside of the region.

The figure below shows how a set of random numbers (generated by sampling from a uniform distribution between 0 and 1) is modified (biased) using the ImpProb function to focus on the specified Target. An unbiased uniform distribution simply produces a CDF Cumulative Distribution Function. The integral of a probability density function. that is a straight line with a slope of 1. The biased distribution of random numbers (in this case with a Target of 0.4 and a Width of 0.05 focuses 50% of the samples to fall between 0.375 and 0.425. The remaining 50% falls outside this range (in this case 20% below and 30% above).

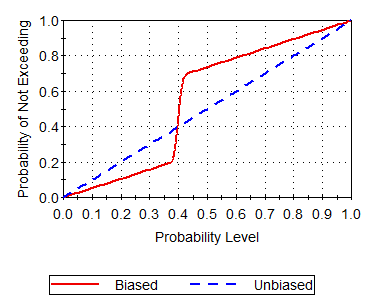
Of course, the weights of these samples are adjusted accordingly (using the ImpWeight function) such that in this case, the 50% of the samples falling between 0.375 and 0.425 account for only 10% of the total weight.

The following points should be noted regarding customized importance sampling:

• The Target must be defined as a value between 0 and 1.
• The Width must be between 1E-6 and 0.5.
• Using the approach outlined above, any correlation factor specified for Stoch1 will be ignored (since the value is not generated by the distribution, but via the PDF_Value function).
• This approach can readily be applied to do enhanced sampling of multiple Stochastic elements. It is simply necessary to 1) use a different (uncorrelated) random number (U in the example above) for each element; and 2) multiply all of the independent realization weights together to generate the Realization Weight used in the Simulation Settings dialog. However, when multiple elements use importance sampling it is important not to use narrow sampling regions, as this can lead to numerous “wasted” realizations that have negligible realization weights.
• The custom importance sampling approach is compatible with the built-in functionality to force importance sampling on either the low end or high end of a Stochastic element's range. Hence, your model could contain some elements that use the "built-in" approach and others that use the custom approach.