Random Choice elements allow you to represent event trees (processes consisting of specified random event sequences).

Random Choice elements have an unlimited number of specified outputs which represent discrete event signals. When the element is triggered, it emits a discrete event signal A discrete signal indicating that something (e.g., an accident, an earthquake, a bank deposit) has occurred. from one (and only one) of its outputs, depending on a set of user-specified probabilities.
The dialog for a Random Choice element An event element that allows you to represent event trees (processes consisting of specified random event sequences). looks like this:
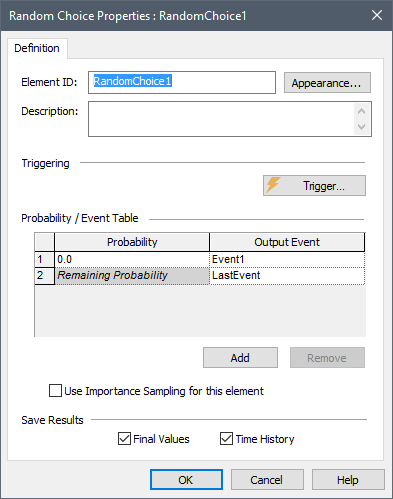
You first specify when the Random Choice is to be triggered via the Trigger... button. The Trigger... button in the Decision dialog provides access to a standard Trigger dialog.
You must then define a set of Probability/Event pairs. That is, you specify the name of an Output Event (a discrete event signal output) and a corresponding Probability.
By default, there are two Output Events, which are named Event1 and LastEvent. The Output Event name can be modified by the user to any string. (Note, however, that the same rules which apply for element names apply for these IDs.)
You can define the Probability for all of the Events, except the last. The probability of the last event is always equal to 1 - (the sum of the other probabilities). The Probability can be specified as a number, links or expression, and can change with time. At all times, however, the specified values must sum to a value less than or equal to 1 (otherwise, a fatal error will be displayed when you run the simulation).
When the element is triggered, it randomly selects one of the Output Events based on the specified discrete probabilities, and emits a discrete event signal from that output.
To understand how a Random Choice element works, consider the following example:
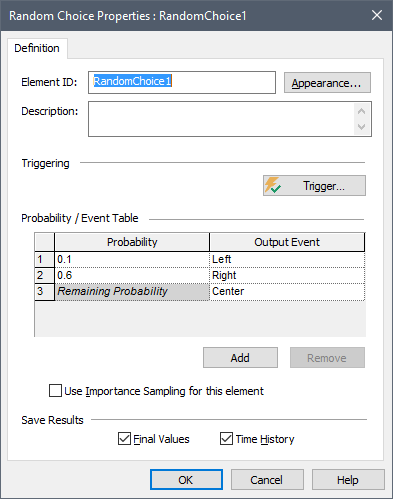
In this case, whenever the element is triggered, GoldSim evaluates the Probabilities, and randomly selects an Output Event based on these Probabilities. In this particular case, there is a 10% chance that it will emit a discrete event signal from the Left output of the element (in this case, named RandomChoice1.Left), a 60% chance that it will emit a discrete event signal from the Right output of the element (in this case, named RandomChoice1.Right), and a 30% chance (1 – 0.1 – 0.6) that it will emit a discrete event signal from the Center output of the element (in this case, named RandomChoice1.Center).
In addition to the discrete event signal outputs associated with a Random Choice element (which you provide a name for), an additional output is produced called Last_Choice. This is a value which takes on an integer value of between 0 and n, where n is the number of Output Events defined. Prior to the Random Choice being triggered, it takes on a value of 0. After the Random Choice is triggered, it records which of the discrete event signal outputs emitted the signal (e.g., if the third event in the list was emitted, Last_Choice would be 3).
Note: A Random Choice element could be triggered multiple times within a single update (e.g., a timestep A discrete interval of time used in dynamic simulations.), in which case it would output multiple events. For each event, it would internally resample the Output Event.
To facilitate these type of analyses, GoldSim allows you to utilize an importance sampling algorithm to modify the conventional Monte Carlo approach so that the high-consequence, low-probability events are sampled with an enhanced frequency. That is, importance sampling serves to increase the rate of occurrence of the event. During the analysis of the results that are generated, the biasing effects of the importance sampling are reversed. The result is high-resolution development of the high-consequence, low-probability "tails" of the consequences (resulting from low-probability events), without paying a high computational price.
Importance sampling for Random Choice elements is specified by selecting the checkbox for Use Importance Sampling for this element. The algorithm that is used is discussed in detail in Appendix B of the GoldSim User’s Guide. For Random Choice elements, when importance sampling is applied, the alternatives are sorted by their probabilities, and the importance sampling serves to artificially bias (increase) the likelihood of the low probability alternatives (such that the least probable choice has the greatest magnification).
Three points regarding importance sampling for Random Choice elements should be noted:
- Importance sampling is only applied to the element the first time it is triggered. The increased sampling frequency for low probability alternatives is not applied to subsequent times the element is triggered in the realization A single model run within a Monte Carlo simulation. It represents one possible path the system could follow through time..
- Importance sampling of Random Choice alternatives should only be used if at least one of the alternatives is rare. As used here, “rare” indicates that an alternative would not adequately be represented without enhanced sampling. As a general rule of thumb, an alternative will be adequately sampled if the product of the number of realizations and the probability of occurrence is at least 10 (this would indicate that the alternative would be expected to be selected at least 10 times if that many realizations were executed). For example, if the probability of an alternative was 0.01 and 100 realizations were run, the total expected number of times the alternative would be selected (over all realizations) would therefore be 1. This is a rare alternative and importance sampling should be applied (or more realizations should be run).
- There is a limit to the effectiveness of importance sampling for extremely rare alternatives, such that in some cases, it may become necessary to increase the number of realizations in order to effectively represent the alternative. In particular, the degree of biasing for low probability alternatives that GoldSim can provide is (at most) equal to the number of realizations. For example, if probability of an alternative was 1e-4, and 100 realizations were run, the total expected number of times that alternative would be selected (over all realizations) would therefore be 0.01. This is a rare alternative and importance sampling should be applied. However, importance sampling could only increase the total number of occurrences (over all realizations) by a factor of 100 (the number of realizations) to 1 (which would still provide inadequate representation). If 1000 realizations were run, the total expected number of occurrences (over all realizations) without importance sampling would be 0.1, but importance sampling would improve it by a factor of 1000. As stated above, the degree of biasing for low probability alternatives that GoldSim can provide is at most equal to the number of realizations. The actual degree of biasing provided decreases with the number of elements for which importance sampling is applied (and the algorithm is discussed in detail in Appendix B of the GoldSim User’s Guide.
The inputs to a Random Choice are the trigger(s) and any associated Precedence or Required Conditions, as well as the Probabilities. Random Choice elements have at least two discrete event signal outputs, along with the Last_Choice output.
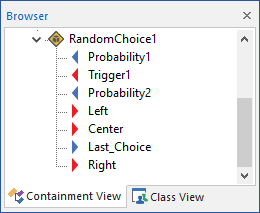
The discrete event signal outputs themselves cannot be saved or viewed as a result.
Note: Element inputs and outputs are only shown in the browser An alternative view of a GoldSim model, in which elements are displayed in a tree, and organized either hierarchically, or by type. if you choose to Show Element Subitems (accessed via the browser context menu by right-clicking in the browser).
The example model RandomChoice.gsm in the General Examples/Events folder of your GoldSim directory (accessed by selecting File | Open Example... from the main menu) contains an example of the use of Random Choice elements.