Applying Importance Sampling to a Stochastic Element

For risk analysis An analysis that focuses on predicting the probability of those (presumably rare) failures that can lead to injury, loss of life, severe damage to the system, or perhaps damage to the surrounding environment., it is frequently necessary to evaluate the low-probability, high-consequence end of the distribution of the performance of the system. Because the models for such systems are often complex (and hence need significant computer time to simulate), it can be difficult to use the conventional Monte Carlo approach to evaluate these low-probability, high-consequence outcomes, as this may require excessive numbers of realizations.

To facilitate this type of analysis, GoldSim allows you to utilize an importance sampling An algorithm that biases sampling of probability distributions in order to better resolve the tails of the distributions. algorithm to modify the conventional Monte Carlo approach so that the tails of distributions (which could correspond to high-consequence, low-probability outcomes) are sampled with an enhanced frequency. During the analysis of the results that are generated, the biasing effects of the importance sampling are reversed. The result is high-resolution development of the high-consequence, low-probability "tails" of the consequences, without paying a high computational price.

Importance sampling is specified by selecting an option from the Importance Sampling button (the default is “None”):

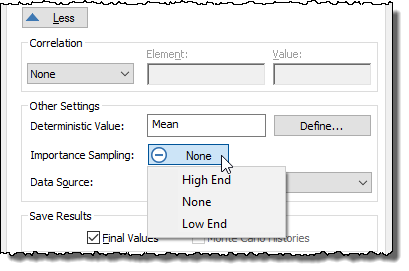
If you select “High-End” GoldSim will preferentially bias toward the high end of the distribution; if you select “Low End”, it will preferentially bias toward the low end of the distribution.

It is important to understand that you should use importance sampling sparingly (i.e., only for those elements that really need it). This is because the degree of biasing for distribution tails that GoldSim can apply decreases with the number of elements for which importance sampling is applied.

The importance sampling algorithm is discussed in detail in Appendix B of the GoldSim User’s Guide.

Note: Importance sampling cannot be applied if the Stochastic is resampled during a realization A single model run within a Monte Carlo simulation. It represents one possible path the system could follow through time..

Note: In addition to the importance sampling method described here (in which you can choose to force importance sampling on either the low end or high end of a Stochastic element An element that can be used to quantitatively represent the uncertainty in a model input.’s range), GoldSim also provides an advanced feature that supports custom importance sampling that can be applied over user-defined regions of the Stochastic element’s range.