Step 6: Computing Reliability and Availability

Although simple time histories of failure for a single realization A single model run within a Monte Carlo simulation. It represents one possible path the system could follow through time. may be of some interest, what we are really interested in doing is computing the reliability and availability The probability that a component or system is performing its required function at any given time. of the Component.

We can view these results by opening the Component's property dialog and viewing the Results tab:

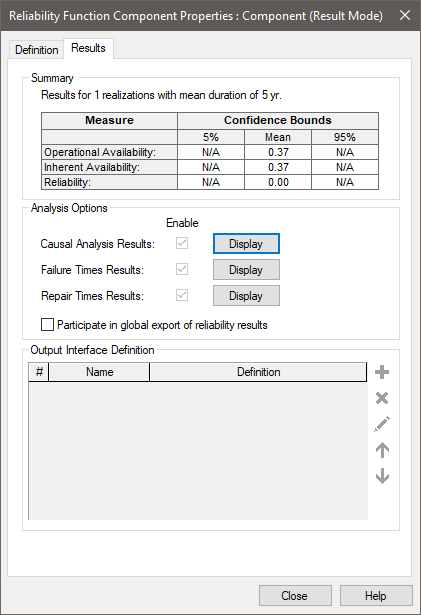
Note: As pointed out previously, your result will be different, since this represents one random realization of the system

The results shown above show an Availability of 0.37 and a Reliability of 0. What does this mean? The problem is that these metrics cannot be accurately determined by running a single realization of the model. The Availability is simply being computed here as the time the Component was operating (in this case about 1.85 years) divided by the total simulation time (5 years). The Reliability is zero because the Component failed in this particular realization.

We cannot draw accurate statistical conclusions with a sample size of one. In order to discern the expected behavior of the system, and the boundaries of that behavior, we need to either run multiple realizations or, if the system was being repaired, run a single realization for a long time so that it models multiple failure and repair cycles. In the next step, we will do the former.