The Overflow_Rate output of a Reservoir A stock element that integrates and conserves flows of materials. has meaning (and is computed) only if you have specified an Upper Bound. GoldSim computes the Overflow_Rate such that the flowing material (e.g., water, widgets, people, rocks) is conserved. To understand how it does so, recall the key assumption regarding the Euler integration A simple and commonly used numerical integration method. method: The specified Rates of Change (Additions and Withdrawal Requests) represent constant rates over the next timestep A discrete interval of time used in dynamic simulations..
Hence, at the beginning of a timestep, GoldSim can project what the Value will be at the end of timestep, compare it to the Upper Bound, and easily compute an Overflow_Rate for that timestep. To illustrate this, consider the following simple example. Assume we are modeling a pond with an Upper Bound of 3000 m3, and that at time = 10 days, the pond contains 2700 m3 of water. Let’s further assume that our model has a 2 day timestep. Assume that for times greater than 10 days, the Additions/Rate of Change and the Withdrawal Requests/Rate of Change are constant and equal to 500 m3/day and 100 m3/day, respectively, so that the pond will fill up and start to overflow at 10.75 days.
In order to compute overflow rates accurately, by default GoldSim inserts an “unscheduled update” when the Reservoir reaches an Upper Bound. Unscheduled updates Timesteps that are inserted automatically by GoldSim during a simulation and are not directly specified by the user prior to running the model. are timesteps that are automatically inserted by GoldSim during the simulation in order to more accurately simulate the system.
In particular, the Overflow_Rate for the example described above is treated as follows. At 10 days, GoldSim would report an (instantaneous) Overflow_Rate of zero. A new timestep (an “unscheduled update”) would then be inserted at 10.75 days when the pond would start to overflow. The Overflow_Rate at this time would actually be internally calculated as 400 m3/day. However, because by default GoldSim only reports values at scheduled timesteps Timesteps that are directly specified by the user prior to running the model. (e.g., 10 days, 12 days), the Overflow_Rate will not be displayed as 400 m3/day until 12 days.
Hence, it is important to understand that the Overflow_Rate represents the instantaneous overflow rate at the reported time. You cannot assume that this rate is constant over the next scheduled timestep. That is, it would be incorrect to assume that the overflow rate was zero between 10 and 12 days. In fact, at 10 days, the overflow rate was indeed 0 m3/day, but it changed to 400 m3/day at 10.75 days (between the scheduled updates). Because 10.75 days is an unscheduled timestep, you would not see this in a time history plot. However, if the Overflow_Rate was integrated (using an Integrator or another Reservoir that represented the total amount of water that has overflowed), the following results would be obtained:
| Time (days) |
Reported Overflow Rate (m3/day) |
Total Water Overflowed (m3) |
| 8 | 0 | 0 |
| 10 | 0 | 0 |
| 12 | 400 | 500 |
| 14 | 400 | 1300 |
Note that the amount of water is properly conserved. At 12 days, the pond has been overflowing for 1.25 days (at a rate of 400 m3/day), so that a total volume of 500 m3 has overflowed. At 14 days, the pond as been overflowing for 3.25 days, so a total volume of 1300 m3 has overflowed.
Note: In some cases, it may be of interest to see the values (such as the Overflow_Rate) that were computed at unscheduled updates. To facilitate this, GoldSim provides an option to do so (under a specified set of conditions) in the Advanced Time settings.
Note: Most spreadsheet models implicitly compute average values (e.g., flows) over a step (or the change from one step to the next). You can compute average values such as these (e.g., in order to compare GoldSim with a spreadsheet model) by using Goldsim’s Reporting Periods Regular time points during a simulation (e.g., every month, every year) at which you can compute and view results associated with that period (e.g., monthly averages, annual cumulative values). feature.
Note: As noted above, by default, GoldSim inserts an unscheduled update when the Reservoir reaches an Upper Bound. However, if desired, you can disable unscheduled updates (although it is generally not recommended). If you do so, the reported Overflow_Rate is the average rate over the next scheduled timestep and can be assumed to be constant. (This option is accessed via the Advanced... button in the Time tab of the Simulation Setting dialog).
Note: You can record when Reservoirs hit or depart from their Upper and Lower Bounds in the model’s Run Log Text that is stored with a GoldSim model once it has been run. It contains basic information regarding the simulation, and any warning or error messages that were generated.. This logging can be activated via the General tab of the Options dialog (accessed via Model|Options from the main menu).
The calculation of an Overflow_Rate is further complicated because the Upper Bound can be specified to change with time (i.e., you could specify this input as being time-variable). If you do so, GoldSim makes the following assumption: like the Rates of Change, the Upper Bound is assumed to remain constant over a timestep.
For example, if you specify that the Upper Bound varies linearly from 3000 m3 to 2000 m3 over 100 days, and simulate the system with a 10 day timestep, GoldSim will approximate the Upper Bound curve internally as a stair-step function:
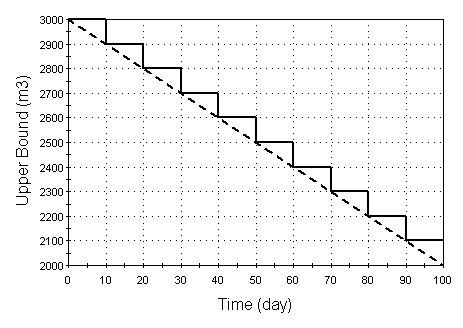
Hence, within a given timestep, GoldSim follows the same logic outlined in the previous example to compute the Overflow_Rate for that timestep.
Note that an Overflow_Rate can be generated even if there is no net inflow of material into the Reservoir. This can happen if the Upper Bound decreases below the Value. To illustrate this, consider the following simple example. Assume we are modeling a pond with an Upper Bound of 3000 m3. Further assume that at the beginning of a timestep, the pond contains 2700 m3 of water. There are no further additions or withdrawals from the pond. However, assume that over the next timestep, the Upper Bound decreases from 3000 m3 to 2500 m3 (e.g., it fills up with silt).
How would GoldSim handle this? During the timestep the Upper Bound would be assumed to remain at 3000 m3. At the beginning of the following timestep, however, it would instantaneously decrease to 2500 m3. This would result in 2700 - 2500 = 200 m3 of water that would instantaneously have to overflow. GoldSim actually spreads this out over the following timestep, such that with a 2 day timestep, the Overflow_Rate over the following timestep would be 200/2 = 100 m3/day.
Note: If the Upper Bound is constant, the Value in the Reservoir will never exceed the Upper Bound. However, if the Upper Bound is changing with time, under some circumstances, it is possible for the Value of the Reservoir to exceed the Upper Bound. If the Upper Bound is exceeded (because it has changed during a timestep), GoldSim will overflow the excess uniformly over the next timestep.
Note: Although GoldSim conserves mass in these situations, this does not imply that the result is perfectly accurate. In fact, the accuracy of the result is a function of the timestep, since GoldSim is approximating continuously varying functions (i.e., rates and bounds) using stair-step functions. This approximation is discussed further in Appendix F of the GoldSim User’s Guide.
Learn more
- Browser View of a Reservoir Element
- Defining Upper and Lower Bounds for a Reservoir
- How a Reservoir Computes its Primary Output
- How a Reservoir Computes the Overflow Rate
- How a Reservoir Computes the Withdrawal Rate
- Instantaneously Replacing the Current Value of a Reservoir
- Modeling Discrete Changes to a Reservoir
- Reservoir Elements
- Specifying Discrete Additions and Withdrawals to a Reservoir
- Specifying the Dimensions, Initial Value and Rates of Change for a Reservoir
- Using the Is_Full Output of a Reservoir
- Using the Withdrawal Rate Output of a Reservoir