The Gamma distribution is similar to a Log-Normal, but is less positively-skewed. Because it mathematically represents the time required for the occurrence of a specified number of Poisson events, it is often used to represent the time required to complete a particular task or reach a particular milestone. It is defined by a Mean and a Standard Deviation:
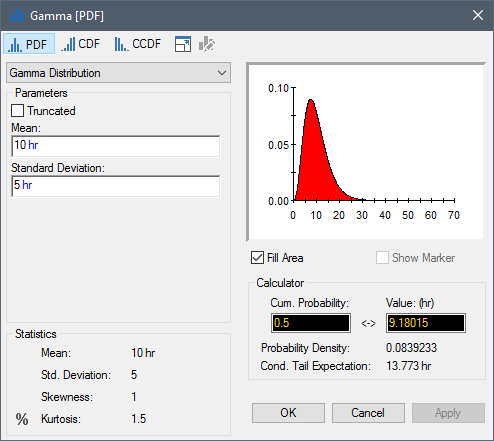
If desired, a Gamma distribution can be Truncated, in which case you must specify a Minimum and Maximum value. Note that in this case, the Mean and Standard Deviation The square root of the variance of a distribution. The variance is the second moment of the distribution and reflects the amount of spread or dispersion in the distribution. inputs refer to the statistics prior to truncation.
Note: If the Mean and Standard Deviation are identical, the Gamma distribution collapses to an exponential distribution.
- Beta Distribution
- BetaPERT Distribution
- Binomial Distribution
- Boolean Distribution
- Cumulative Distribution
- Discrete Distribution
- Exponential Distribution
- Externally-Defined Distribution
- Extreme Probability Distribution
- Extreme Value Distribution
- Gamma Distribution
- Generalized Beta Distribution
- Log-Normal Distribution
- Negative Binomial Distribution
- Normal Distribution
- Pareto Distribution
- Pearson Type III Distribution
- Poisson Distribution
- Sampled Results Distribution
- Student’s t Distribution
- Triangular Distribution
- Uniform Distribution
- Weibull Distribution