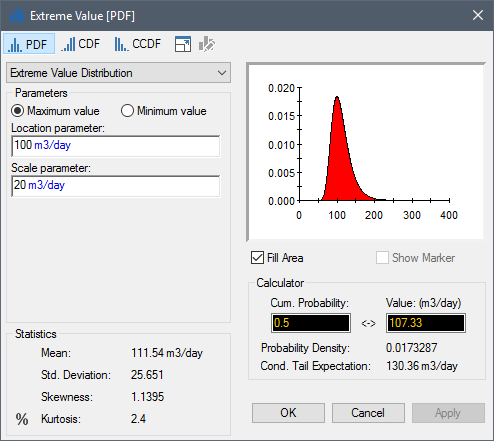
The Extreme Value distribution (also referred to as the Gumbel distribution) is a continuous distribution used to describe the maximum (or the minimum) observed values for a variable. For example, you could use this distribution to specify the probability of the maximum flow rate in a river in a particular year by fitting a list of the maximum values observed for each of the past 25 years to this distribution. It is therefore commonly used to predict the chance of extreme events such as earthquakes or floods.
It is defined by specifying two parameters: a Location parameter and a Scale parameter. You must also specify whether you are interested in the Maximum value or the Minimum value:
- Beta Distribution
- BetaPERT Distribution
- Binomial Distribution
- Boolean Distribution
- Cumulative Distribution
- Discrete Distribution
- Exponential Distribution
- Externally-Defined Distribution
- Extreme Probability Distribution
- Extreme Value Distribution
- Gamma Distribution
- Generalized Beta Distribution
- Log-Normal Distribution
- Negative Binomial Distribution
- Normal Distribution
- Pareto Distribution
- Pearson Type III Distribution
- Poisson Distribution
- Sampled Results Distribution
- Student’s t Distribution
- Triangular Distribution
- Uniform Distribution
- Weibull Distribution