The Extreme Probability distribution is a continuous distribution used to represent the uncertainty in the highest or lowest probability level if any given distribution is sampled N times. As such, the Extreme Probability distribution represents the probability distribution of a probability level, and therefore always ranges between 0 and 1.
It is defined by specifying the Number of samples, and whether you are interested in the probability level for the Maximum value or the Minimum value:
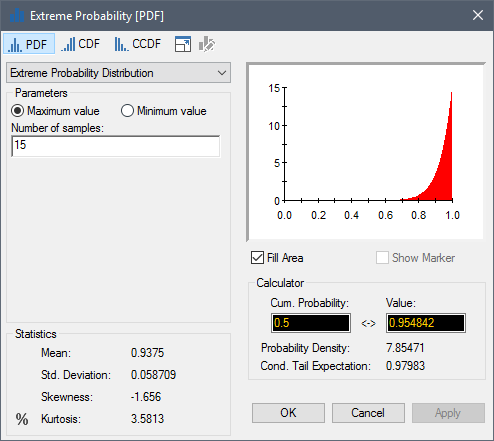
The input must be a positive value. The displayed distribution represents the probability of the maximum or minimum value corresponding to a particular probability level given a specified number of samples. For example, in the screen shown above, the distribution represents the uncertainty in the probability level of the maximum value assuming 15 samples. It indicates that the expected value of the maximum probability level is 0.9375.
Note: The Extreme Probability distribution must always be dimensionless, as it represents a probability level (otherwise GoldSim will display an error).
- Beta Distribution
- BetaPERT Distribution
- Binomial Distribution
- Boolean Distribution
- Cumulative Distribution
- Discrete Distribution
- Exponential Distribution
- Externally-Defined Distribution
- Extreme Probability Distribution
- Extreme Value Distribution
- Gamma Distribution
- Generalized Beta Distribution
- Log-Normal Distribution
- Negative Binomial Distribution
- Normal Distribution
- Pareto Distribution
- Pearson Type III Distribution
- Poisson Distribution
- Sampled Results Distribution
- Student’s t Distribution
- Triangular Distribution
- Uniform Distribution
- Weibull Distribution