In some cases, it may be necessary to represent a
recirculating system (e.g., a system in which water or some other material recirculates in a loop). Under some
circumstances, if you try to create such a system, GoldSim may prevent you from “closing” the loop by reporting that the system is recursive. GoldSim can
represent such looping systems, but in order to do so, the loop must contain a
This is best illustrated by examining a simple example.
Note: For simplicity, this example uses Reservoirs, but it could just as easily have used Pools.
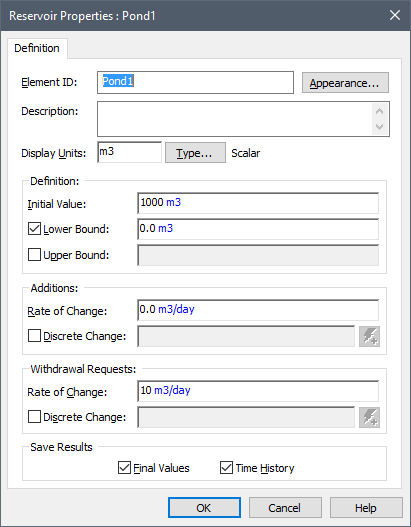
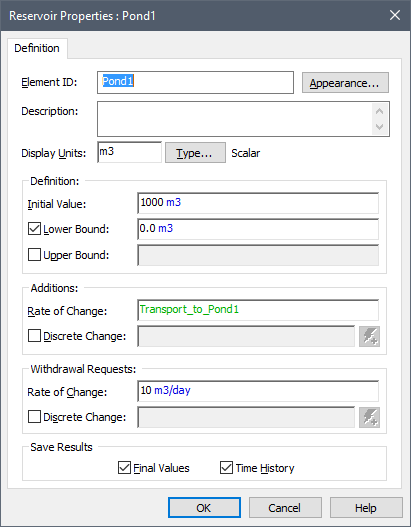
Consider a system consisting of two ponds. The first pond (Pond1) has an initial volume (Initial Value) of 1000 m3 and a Withdrawal Request (due to pumping) of 10 m3/day:
The second pond (Pond2) accepts the Withdrawal_Rate output from Pond1 as an Addition and has an Upper Bound of 400 m3:
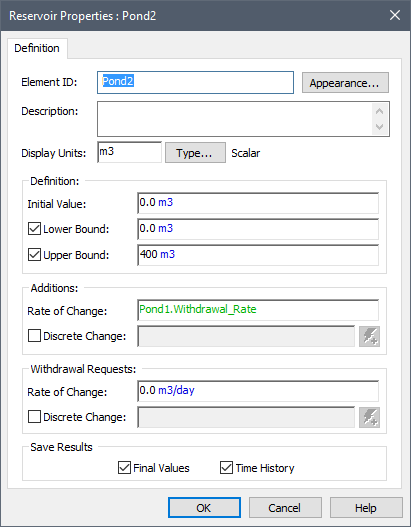
Because Pond2 has an Upper Bound, it has an Overflow_Rate output.
What we would like to do is route the overflow from Pond2 back into Pond1, hence creating a recirculating system: water is pumped from Pond1 into Pond2, and when Pond2 overflows, it is directed back into Pond1. Logically, there is nothing at all wrong with this system. However, if you try to do this (by routing the Overflow_Rate from Pond2 as an Addition for Pond1, the following error is displayed:
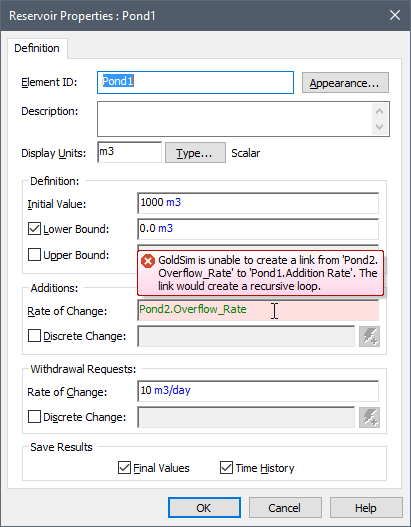
GoldSim is unable to create this link, because it would form a loop that contains no state variables. All loops in GoldSim must contain a state variable. (There are no state variables in the loop because neither the Withdrawal_Rate output nor the Overflow_Rate output is a state variable.)
Fortunately, we can address this by inserting a Material Delay element into this loop. In particular, we can define the Overflow_Rate from Pond2 as the input to a Material Delay:
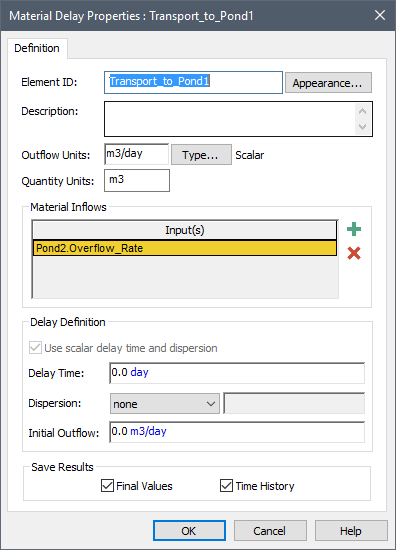
We can then define the output for the Material Delay as the Addition to Pond1, thereby closing the loop:
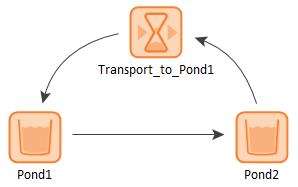
This works because the output of a Material Delay is a state variable.
But what does this mean physically? It simply means that when water overflows from Pond2 it does not enter Pond1 immediately. There is a delay while it is transported there. In fact, we could also add a Material Delay between Pond1 and Pond2, as there is likely some kind of delay there also. What is the appropriate delay time? If we leave it at zero, GoldSim will use the timestep length as the delay time. That is, material cannot move through a Material Delay in less than a timestep. This would be appropriate if the actual travel time was quite short. (This introduces a slight error if the actual delay time is significantly less than a timestep. If this is important to represent, it would be necessary to shorten the timestep). If the travel time is greater than a timestep, the actual travel time should be entered.
Learn more
- Browser View of a Material Delay Element
- Material Delay Elements
- Material Delays with Time-Variable Delay Times
- Mathematics of Material Delays
- Modeling Material Delays with Dispersion
- Modeling Material Delays without Dispersion
- Representing a Material Delay with an Inflow Limit
- Specifying Initial Outflows for Material Delays
- Specifying the Inputs to a Material Delay
- Using Material Delays to Close Feedback Loops and Model Recirculating Systems