Simple models have a direct chain of causality: input data affect some elements, which affect other elements, and so on, until eventually the elements that calculate the desired results of the model are reached:

GoldSim automatically analyzes your entire model to identify "who affects who", and ensures that the "upstream" elements are calculated prior to the "downstream" elements. At each timestep A discrete interval of time used in dynamic simulations. the elements are updated in this causality-based sequence.
Most real-world models, however, contain elements whose output can, directly or indirectly, affect one of their own inputs. This creates a looping or circular system such as the one shown below:
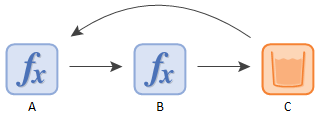
These types of systems are referred to as
GoldSim allows you to create looping systems like this. In order to do so, however, the loop must meet one requirement: it must contain at least one
In the simple looping example above, A references the primary output For an element with multiple outputs, the output that has the same name as the element. (a state variable) of C. Let’s also assume that B represents the Rate of Change (an addition) to C.
Every timestep, after changing the system clock, GoldSim first updates the state variable outputs that are intrinsic functions of time. In this example, the only element that falls into this category is the Reservoir A stock element that integrates and conserves flows of materials. named C. Its primary output is a state variable. So the primary output for C is first brought up to the current time (based on the value of B at the end of the previous timestep).
After doing this, GoldSim then updates the elements according to the causality sequence The specific order in which GoldSim updates (computes) elements every timestep.. If we were to view the causality sequence for the system above, it would look like this:
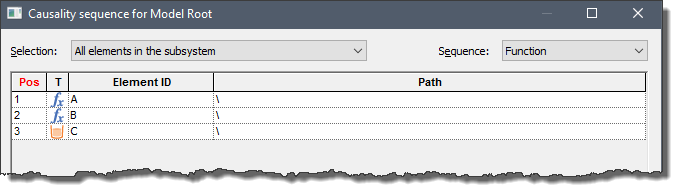
So first GoldSim computes A (based on the updated value of the primary output of C). Then it computes B. Finally, GoldSim updates C again.
Why is C updated twice (prior to evaluating the causality sequence and then again at the end of the causality sequence)? In this simple example, it is because C has multiple outputs, not all of which are state variables (e.g., the Withdrawal_Rate). These non-state variables need to be updated here at the end of the causality sequence. Moreover, during this update, C stores the new input for B for use the next time the clock is advanced.
Note: In some cases, GoldSim may not be able to create a valid sequence at all. This is the result of the system having circular (recursive) logic without a state variable involved. GoldSim can still represent such systems, but in order to do so, it is necessary for you to explicitly add a state variable to the system.
More information on feedback loops is provided in the