Defining a Proportional Integral Derivative (PID) Controller

A Proportional Integral Derivative (PID) Controller is the most complex (and powerful) of the methods. Like the Proportional Controller, it continuously adjusts the output as a function of the error. Unlike that Controller, however, in which the adjustment is a simple function of the error, the adjustment for a PID Controller depends not only on the error, but on the integral and derivative of the error.

As is the case for the Proportional Controller, the error is the difference between the current value of the process variable and the target. How the error is calculated is a function of whether the Controller is an Inflow or Outflow Controller:

• Outflow Controllers: Error = Process Variable – Target
• Inflow Controllers: Error = Target – Process Variable

The output is then computed as follows:

Output = Min (Max (Bias + PID Sum, 0) , Flow Capacity)

where PID Sum is the sum of three different terms:

Bias, Proportional Gain, Integral Gain, Derivative Gain and Flow Capacity are user-defined inputs.

The integral term (I) increases in relation not only to the error but also the time for which it has persisted. Hence, if the error does not reverse and become negative this term will be increase as time passes. As such, the intregral term represents the “impatience” of the Controller. The derivative term uses the rate of change of the error to manipulate the Controller output with the intent to reduce overshoot and oscillation. This term is intended to counteract rapid changes in the process variable and moderate the speed at which it changes. Hence, in contrast to integral term, which represents the “impatience” of the Controller, the derivative term represents the “caution” of the Controller in that it works to limit how fast the output can change. Note that the derivative term does not consider the magnitude of the error, and as a result can not by itself bring the error to zero.

GoldSim starts by computing the output as Bias + PID Sum. Note, however, that there are two constraints imposed:

• The output cannot be less than zero. This could happen if the PID Sum was sufficiently negative.
• The output cannot be greater than the Flow Capacity.

Hence, when you select “PID” as the Method, there are five additional inputs that must be provided:

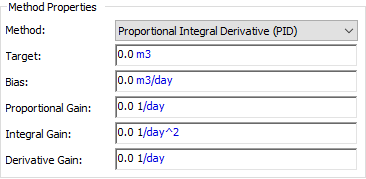
Target: This is the desired value of the process variable. Hence, it must have the same dimensions An output attribute for an element that defines the dimensionality (in terms of Length, Time and other fundamental dimensions) of the output. as the process variable (Flow Units * Time). While the Target is often constant, it can be specified to change with time.

Bias: This is the value of the output when the PID Sum term is zero (which can be non-zero even if the error itself is zero). As such, it is difficult to assign a physical meaning to this term (it is simply a “tuning parameter”). Note that the Bias tends to only impact behavior at early times (before the Gain terms can adjust the output).

Proportional Gain: This has dimensions of inverse time, and represents how strongly the “P” term in the sum to responds to the error. The larger this number, the quicker it responds.

Integral Gain: This has dimensions of the inverse time squared, and represents how strongly the “I” term in the sum to responds to the integral of the error. The larger this number, the quicker it responds.

Derivative Gain: This is dimensionless, and represents how strongly the “D” term in the sum responds to the derivative of the error. The larger this number, the quicker it responds.

Note: If the Integral Gain and the Derivative Gain are set to zero, then a PID Controller becomes a Proportional Controller.

The Bias and the three Gain constants can be thought of as tuning parameters. These values are “tuned” or calibrated to achieve the required performance. They are intended to be constants.