In a Proportional Controller, if the uncontrolled inflows and outflows follow a trend or pattern, a constant Bias would result in poor performance and you would need to take the extra step of defining the Bias as being time variable in order for the Controller to perform well. This is not the case for PID Controllers, which can adjust to trends or changes in the uncontrolled inflows and outflows.
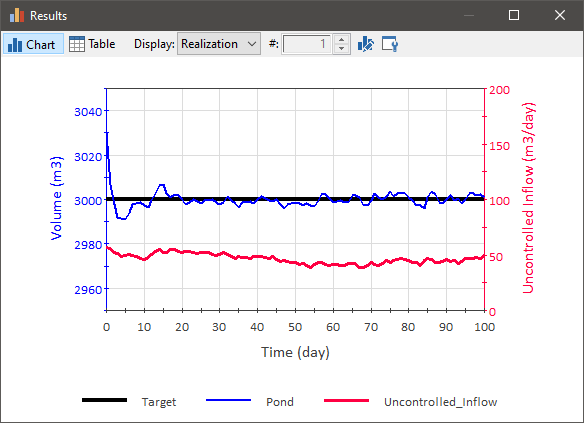
Here, for example, is the performance of a PID Controller in a situation in which there is a “noisy” inflow of water to a pond that changes daily (with a mean of 50 m3/day) , and the PID Controller is an Outflow Controller. The goal is to maintain the volume near a target of 3000 m3 (the initial value is 3030 m3):
And here is the performance of a PID Controller in a situation in which we have an Outflow Controller and the pond has an uncontrolled inflow that is steadily increasing (and is noisy):
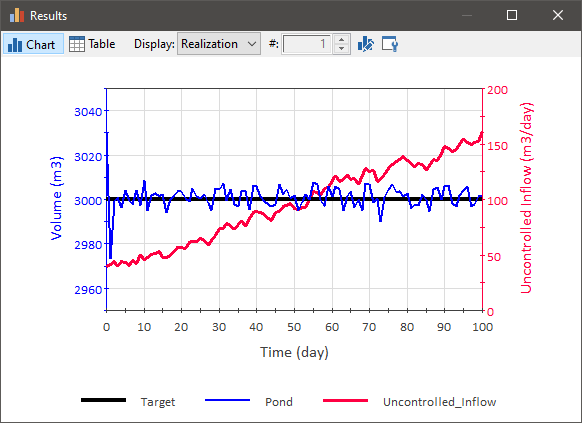
As can be seen, the PID Controller performs well in both cases.
Note: These two examples are actually “tuned” slightly differently. This illustrates the are are truly “tuning” parameters and need to be experimented with for each system. In fact, even in these examples, it is likely that with some effort, the parameters could be further tuned to provide slightly better performance.
Does the timestep A discrete interval of time used in dynamic simulations. affect the performance of the Controller? Conceptually, a Controller is something that is being updated “continuously”. Of course, in a simulation model The implementation of a mathematical model of a system within a specific computational tool (or set of tools)., things are only updated on timesteps. So the timestep does indeed have an impact (the smaller the timestep, the closer the corrections are to being “continuous”). Here is the same model as shown above (with trending inflow) with a 0.1 day timestep (instead of 1 day):
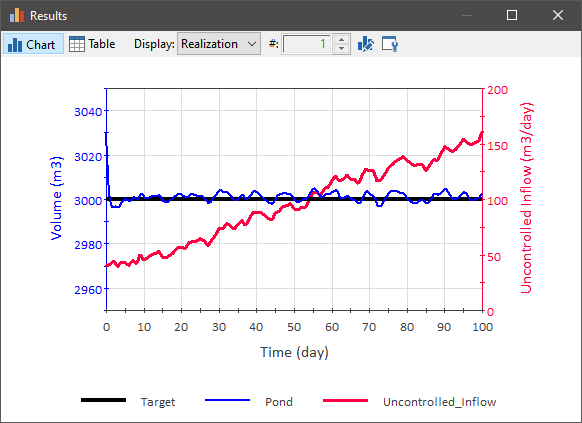
As can be seen, the process variable changes in a smoother manner (since the outflow is updated more frequently), and the performance is considerably better.
One additional aspect of the PID Controller is important to understand: The integral term for the Controller increases in relation not only to the error but also the time for which it has persisted (since it is the integral of the error). Hence, if the error does not reverse and become negative that term will increase as time passes. In most cases, the error will eventually becomes small (and in some cases negative as it moves above and below the target). However, in cases where you are temporarily unable to fully control the process variable (e.g., if uncontrolled inflows were temporarily greater than the Flow Capacity for an Outflow Controller), the integral term would continually increase, and when the uncontrolled inflows final decreased so that you could regain control, the resulting Controller output may remain unrealistically high for some time due to the high integral term (resulting in it overshooting the target).
To understand this, consider the following example. In this model, there is an uncontrolled inflow that starts at about 50 m3/day, increases for a period of 10 days to about 100 m3/day, and then falls to back to 50 m3/day. A PID Outflow Controller attempts to control the outflow to maintain the target volume. However, the Controller has a Flow Capacity of only 75 m3/day:
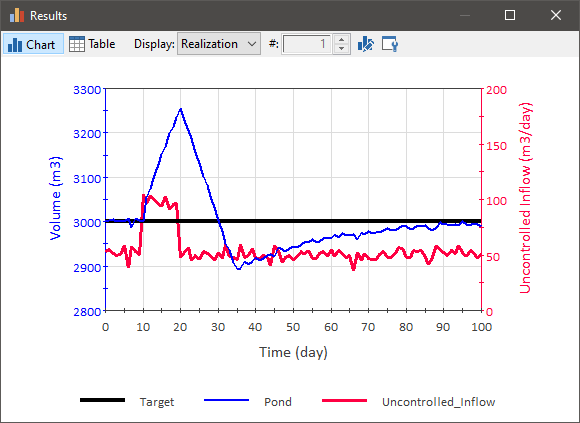
As can be seen, for the 10 days that the uncontrolled inflow is at 100 m3/day, it is unable to control it (due to the limited Flow Capacity). Once the uncontrolled inflow drops such that the Controller can regain control, the Controller brings the volume down toward the target, but temporarily overshoots (due to the integral term) and then gradually approaches the target.
An example model which illustrates the basic use of the PID Controller (PID.gsm), in particular the cases discussed in this