Creating a Stochastic Vector

GoldSim allows you to define a Stochastic element An element that can be used to quantitatively represent the uncertainty in a model input. as a vector A one-dimensional array. of data. If you define your element as a vector, rather than inputting a single probability distribution A mathematical representation of the relative likelihood of a variable having certain specific values. It can be expressed as a PDF (or a PMF for discrete variables), CDF or CCDF., you specify a set of distribution parameters (one for each item of the vector).

To define your element as a vector, press the Type... button on the dialog. The following dialog will appear:

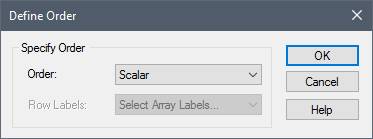
From the Order drop-list select “Vector (1-D Array)”. You will then need to specify a set of Row Labels.

If you specify the Stochastic as a vector, the dialog for defining the distribution (accessed via the Edit Distribution... button) will look similar to this:

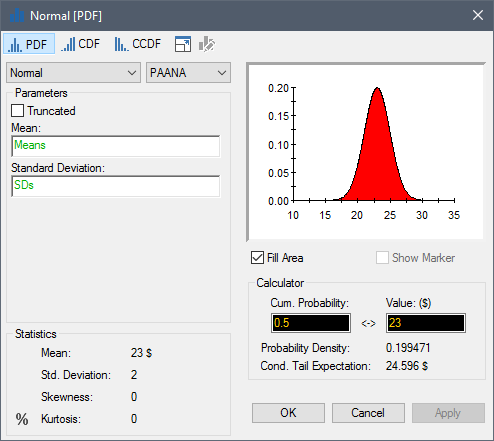
This dialog is identical to the standard dialog for a scalar An output consisting of a single value or condition. Stochastic, with two exceptions:

• The input fields for the parameters for the distribution must be vectors. Hence, when you create a Stochastic vector, all of the items of the vector have the same distribution type, but may have different values for the input parameters for the distribution.

• You view the distribution and the statistics for a particular item of the vector by selecting the item from the drop-down list at the top of the dialog (immediately to the right of the distribution type).

Note: If the distribution type is Cumulative, Discrete or Sampled Results, you cannot enter vectors into the grids defining the distribution. That is, the grids only accept numbers. As a result, all items of the vector would be identical. If you want to create a vector of Stochastics that consists of Cumulative, Discrete or Sampled Results distributions, you can do so by creating a separate Stochastic for each item, and then using a Data element An input element intended to represent constant inputs in a model. (defined as a vector) to reference each separate item.

A Stochastic vector cannot be autocorrelated. It can, however, be correlated to another Stochastic. If the other Stochastic is a vector, the correlation is term-by-term. If the other Stochastic is a scalar, all terms are correlate to the scalar value.

You can also specify correlations between members of the vector via a correlation matrix. A correlation matrix specifies the correlations between variables, and generally has the following form:

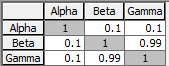
Note that by definition, a correlation matrix is symmetric around its diagonal (since the cross diagonal terms define the same correlation coefficient).

If you specify that a Stochastic is a vector, then the drop-list in the Correlation section of the dialog provides an option called "Matrix". If this option is selected, a button is provided (Define...) to define the correlation matrix:

This button provides access to a dialog for specifying the correlation matrix:

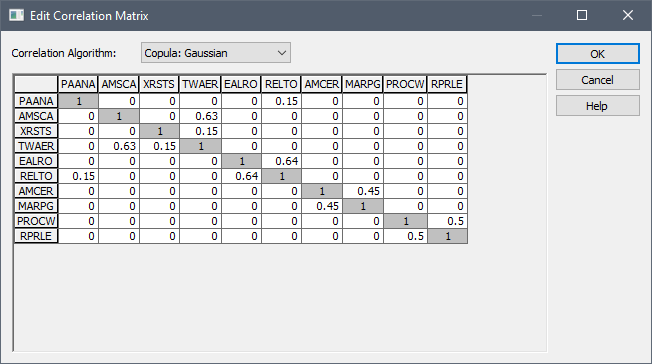
As pointed out above, by default, all off-diagonal correlation coefficients are zero. The matrix is symmetrical, so you need only define one of the cross-diagonal terms. The value represents a rank correlation coefficient, and must vary between -1 and 1. It must be a number (i.e., you cannot specify a link).

Note: When you define a correlation matrix, it is important to ensure that it is internally consistent. For example, if you specified that A was positively correlated to B, and B was positively correlated to C, but that A was negatively correlated to C, the correlation matrix would be inconsistent (since in this case, A should also be positively correlated to C). When this occurs, GoldSim will produce a fatal error message.

GoldSim provides several different algorithms for correlating the members of the vector. These are selected from the Correlation Algorithm drop-list at the top of the dialog. The various correlations algorithms are discussed in Appendix B of the GoldSim User’s Guide.