A History Generator An element that generates stochastic time histories of variables. A stochastic time history is a random time history that is generated according to a specified set of statistics. can be specified to represent a 1-D array A collection of variables that share common output attributes and can be manipulated in GoldSim elements or input expressions. of variables (i.e., a vector A one-dimensional array.). In this case, the various input parameters must be specified as vectors.
This most common application of this is to simulate an array of correlated variables (e.g., a portfolio of investments). When variables are correlated, their random movements (as typically quantified by the volatility) are linked to a greater or lesser degree. For example, consider the three time series below:
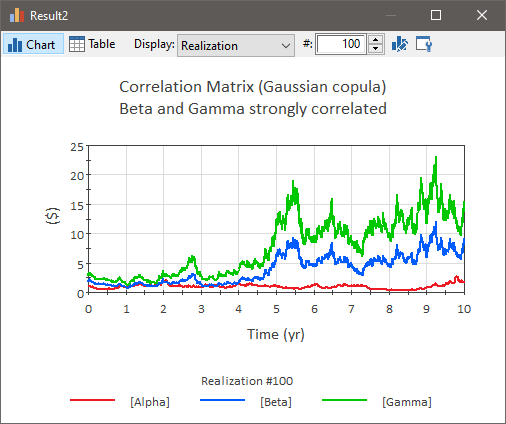
In this example, the volatile movements of Beta and Gamma are strongly correlated, and are both uncorrelated to Alpha.
The correlations between the members of an array are specified via a correlation matrix A two-dimensional array.. A correlation matrix specifies the correlations between variables, and generally has the following form:
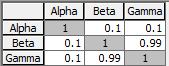
Note that by definition, a correlation matrix is symmetric around its diagonal (since the cross diagonal terms define the same correlation coefficient).
If you specify that the History Generator represents a 1-D array of variables (i.e., a vector), then the Use correlation matrix checkbox becomes available on the History Generator dialog:
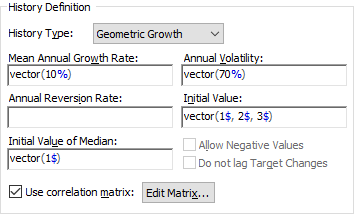
If this box is checked, the Edit Matrix... button becomes available. This button provides access to a dialog for specifying the correlation matrix:
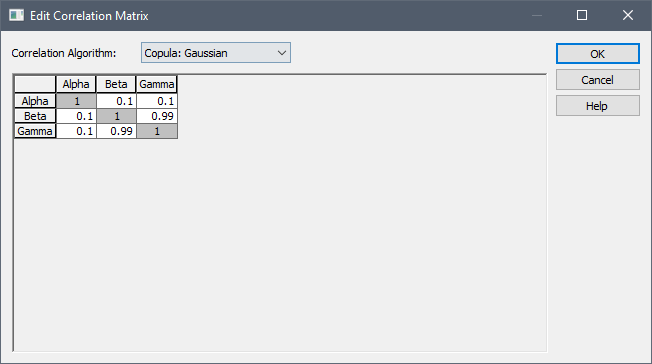
By default, all off-diagonal correlation coefficients are zero. The matrix is symmetrical, so you need only define one of the cross-diagonal terms. The value represents a rank correlation coefficient, and must vary between -1 and 1. It must be a number (i.e., you cannot specify a link).
Note: When you define a correlation matrix, it is important to ensure that it is internally consistent. For example, if you specified that A was positively correlated to B, and B was positively correlated to C, but that A was negatively correlated to C, the correlation matrix would be inconsistent (since in this case, A should also be positively correlated to C). When this occurs, GoldSim will produce a fatal error message.
GoldSim provides several different algorithms for correlating the members of the vector. These are selected from the Correlation Algorithm drop-list at the top of the dialog. The various correlation algorithms are discussed in Appendix B of the GoldSim User’s Guide.