By default, the standard deviation The square root of the variance of a distribution. The variance is the second moment of the distribution and reflects the amount of spread or dispersion in the distribution. of a random walk type history increases with the square root of time. In some cases, when simulating such a history, you may not want the standard deviation to grow with time. Rather, you may want it to stabilize to a constant value around an underlying target.
You can accomplish this by forcing the stochastic history to revert towards a target value at a specified rate. To do so, you must use the Annual Reversion Rate and Target input fields.
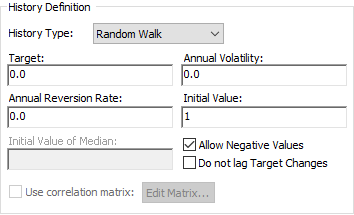
Target. This is the underlying target that the history will revert to (i.e., track). It can be a constant value or a function of time. It has the same dimensions An output attribute for an element that defines the dimensionality (in terms of Length, Time and other fundamental dimensions) of the output. as the output. It can take on any value.
Annual Reversion Rate. This is the annual fractional rate at which the history reverts to its target. Although this is a rate, because it is "hard-wired" to an annual value, this input is dimensionless. That is, it represents the fractional rate per year. It must be non-negative.
If the Annual Reversion Rate is non-zero, GoldSim generates successive values as follows:
where Vnew is the new value, Vold is the previous value, Δt is the time (in years) between the two values, ε is a random standard normal value (sampled from a distribution with mean 0 and standard deviation 1), r is the reversion rate, and σ is the volatility. Tnew is the current (new) value of the underlying target (which may change with time).
In practical terms, specifying a non-zero Annual Reversion Rate has two effects:
- The history tracks the target, and if the Initial Value differs from the initial value of the Target, the history approaches the target history with a half-life of ln(2)/Annual Reversion Rate.
- The standard
deviation initially grows, but eventually stabilizes to a constant value with a
similar half-life. The "steady-state" standard deviation stabilizes at a
value of:
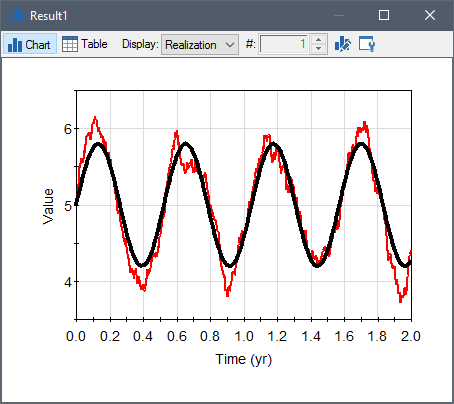
By default, when an Annual Reversion Rate is specified, the history actually lags the target, and as a result, the signal is "dispersed" such that the peaks and valleys of the history are (on average) smaller than that of the target:
The time lag increases as the Annual Reversion Rate decreases.
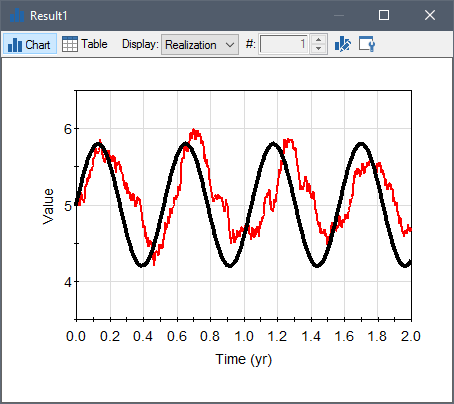
In some cases, you may not want such a time lag. The Do not lag Target Changes checkbox (if checked) eliminates this lag. In this case, GoldSim generates successive values as follows:
As can be seen below, this has the impact of eliminating the lag (and the dispersion):