Selecting "Random Walk" for the History Type field of a History Generator An element that generates stochastic time histories of variables. A stochastic time history is a random time history that is generated according to a specified set of statistics. element allows you to define a history that randomly walks through time.
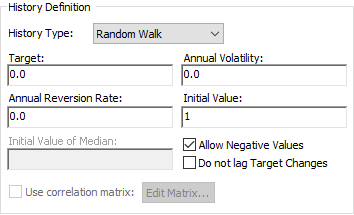
In its simplest form, this type of history requires two
inputs (Annual Volatility, and Initial Value). The other two
inputs (Target and Annual Reversion Rate) are only required if you
wish the history to track an underlying target or trend (and this is discussed
in the next
Annual Volatility. This is the standard deviation The square root of the variance of a distribution. The variance is the second moment of the distribution and reflects the amount of spread or dispersion in the distribution. of the annual values (σ):
where μ is the mean of the annual values:
If the volatility is measured over a different time period (e.g., monthly), this can be scaled by direct multiplication. For example a mean monthly volatility can be converted to a mean annual volatility by multiplying it by √12.
It has the same dimensions An output attribute for an element that defines the dimensionality (in terms of Length, Time and other fundamental dimensions) of the output. as the output, and must be non-negative.
Initial Value. This is the initial value of the time history (the value at time zero). It has the same dimensions as the output and can be positive, negative or zero.
You can control whether your history can take on negative values using the Allow Negative Values checkbox (which defaults on). If this box is cleared, negative values are "truncated". Note that this has the effect of artificially reducing the standard deviation of the values.
If the Annual Reversion Rate is set to zero (the default), GoldSim generates successive values as follows:
where Vnew is the new value, Vold is the previous value, Δt is the time (in years) between the two values, ε is a random standard normal value (sampled from a distribution with mean 0 and standard deviation 1), and σ is the volatility.
For constant values of the Annual Volatility, this results in a history whose standard deviation increases as the square root of time.
