In some types of aging chains, you would like to instantaneously "graduate" all the members of one cohort to the next cohort at a specific time (e.g., every year), and repeat the process for all cohorts. For example, if you had 6 age groups, at the beginning of each year, you might want to transition all the age groups to the next cohort (e.g., cohort 5 graduates to cohort 6, cohort 4 graduates to cohort 5, cohort 3 graduates to cohort 4, etc.).
To facilitate this, GoldSim provides specialized capabilities for Discrete Change and Integrator elements.
One of the Instruction options for a Discrete Change transaction is a "Push":
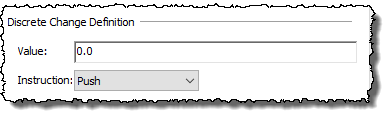
Push instructions can subsequently be processed by Integrators (by specifying the discrete change output as an input in the Discrete Change input field of the Integrator).
Note: Push discrete change outputs can only be processed by Integrator elements. Splitters and Allocators can also accept Push discrete changes, as they don't actually process them; they simply pass them on (preserving the instruction). However, directing a Push discrete change to any other element (e.g., a Reservoir A stock element that integrates and conserves flows of materials.) will result in a fatal error.
When processing a Push discrete change signal A discrete signal that contains information regarding the response to an event., you must specify (under the Advanced options for an Integrator) that the Integrator itself, in turn, provides a"Pushed_Out" discrete change output:
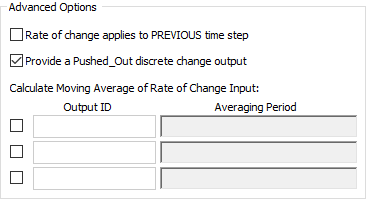
Doing so adds a new output called "Pushed_Out" to the element.
When an Integrator receives a Push discrete change signal (and the "Provide a Pushed_Out discrete change output" is checked), the following occurs:
- The current value of the Integrator is instantaneously "pushed out" and replaced with value specified by the incoming discrete change signal.
- The element produces a discrete change output named "Pushed_Out" that has a "Push" Instruction and a Value equal to the value of the Integrator prior to receiving the discrete change signal. This can subsequently be directed to another Integrator.
Note: If the "Pushed_Out" output is not directed to another Integrator, it still “leaves” the Integrator, but the value that should have been pushed is “lost” from the system.
Note: If you direct a Push discrete change signal to an Integrator in which to "Provide a Pushed_Out discrete change output" is not checked, it acts like an Add signal for that Integrator.
By creating a series of Integrators connected by Push discrete changes (triggered, for example, once per year), you can create an aging chain that instantaneously "graduates" all the members of one cohort to the next cohort at a specific time (e.g., every year). The structure would look something like this:
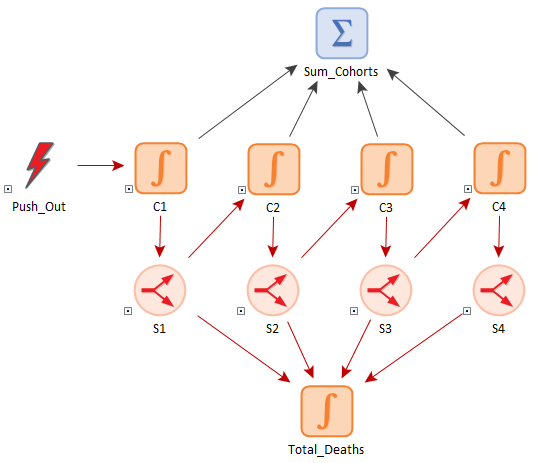
Note that each Integrator does not push into the next Integrator in the series. Rather, it flows through a Splitter An element that splits an incoming signal between a number of outputs based on specified fractions or amounts. Typically, the signal will be a flow of material (e.g., water), but it could also be a resource, or a discrete transaction., so that losses (e.g., due to deaths) can be accounted for prior to graduating to the next cohort. The Integrator representing one of the cohorts would look like this:
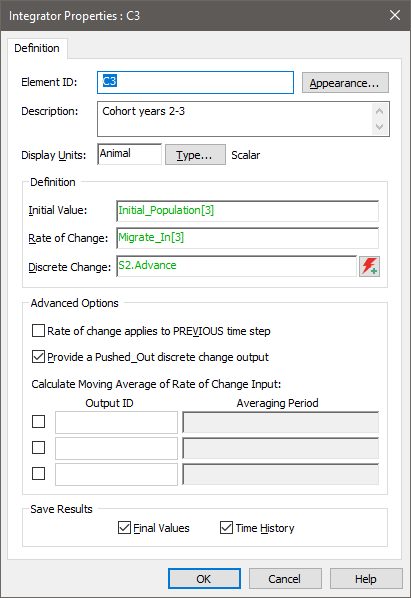
Note: When a scalar An output consisting of a single value or condition. Integrator receives a Push discrete change signal and the "Provide a Pushed_Out discrete change output" is NOT checked, the discrete change is treated as if it had an Add instruction (since it has nowhere to "push" the current value). Hence, the Integrator simply accumulates the changes.
An example file which illustrates how aging chains can be modeled (AgingChain.gsm) using a series of scalar Integrators can be found in the General Examples folder in your GoldSim directory (accessed by selecting File | Open Example... from the main menu).
Although this type of approach can represent specific age groups very accurately, it can be cumbersome if there are a large number of groups. An alternative to this approach that is much better at simulating a large number of age groups is to use an Integrator array A collection of variables that share common output attributes and can be manipulated in GoldSim elements or input expressions. that processes discrete pushes.
In this approach, instead of using a series of Integrators, you use a single Integrator that is a vector A one-dimensional array.. A discrete change signal with a Push instruction is sent to the Integrator. When it receives the instruction, the Value associated with the discrete change is "pushed" into the first item of the vector. Each value in the vector is then pushed downward to the next item of the vector. That is, the value that was in item 1 is pushed to item 2; the value that was in item 2 is pushed to item 3, and so on.
If "Provide a Pushed_Out discrete change output" is checked for the Integrator, the element produces a discrete change output named "Pushed_Out" that has a "Push" Instruction and a Value equal to the value of the last item in the Integrator vector prior to receiving the discrete change signal. This can subsequently be directed to another Integrator. If "Provide a Pushed_Out discrete change output" is NOT checked for the Integrator, the final item in the Integrator vector accumulates all of the "pushes" that it receives.
When implementing such a vector aging chain, the Discrete Change element that generates the initial "push" into the Integrator must be defined in a specific manner. In particular, it must be defined as follows:
- The Instruction must be "Push";
- The Value must be a scalar value; and
- The Type must be defined to match the Type of the Integrator that will receive the discrete change. Hence, although the Value itself is a scalar (since it represents the value being pushed into the first item of the vector), the Discrete Change element must be defined as a vector (as it will be an input to a vector Integrator).
An example of this is shown below:
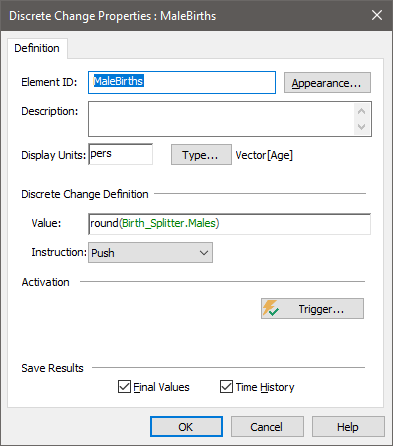
This approach allows you to replace a series of Integrators with a single vector Integrator, and therefore facilitates simulation of chains with a large number of cohorts.
An example file which illustrates how aging chains can be modeled (AgingChainArray.gsm) using a vector Integrator can be found in the General Examples folder in your GoldSim directory (accessed by selecting File | Open Example... from the main menu).
This approach can be extended to utilize a matrix A two-dimensional array. Integrator. In this case, a discrete change signal (whose Value is defined as a vector) with a Push instruction is sent to the Integrator. When it receives the instruction, the Value associated with the Discrete Change is "pushed" into the first row of the matrix. Each row in the matrix is then pushed downward to the next row of the matrix. That is, the values that were in row 1 are pushed to row 2; the values that were in row 2 are pushed to row 3, and so on.
If "Provide a Pushed_Out discrete change output" is checked for the Integrator, the element produces a discrete change output named "Pushed_Out"that has a Push Instruction and a Value equal to the value of the last row in the Integrator matrix prior to receiving the Discrete Change signal. This can subsequently be directed to another Integrator. If "Provide a Pushed_Out discrete change output" is NOT checked for the Integrator, the final row in the Integrator matrix accumulates all of the "pushes" that it receives.
When implementing such a matrix aging chain, the Discrete Change element that generates the initial "push" into the Integrator must be defined in a specific manner. In particular, it must be defined as follows:
- The Instruction must be "Push";
- The Value must be a vector having the same Array Label Set as the columns of the matrix into which it is being pushed ; and
- The Type must be defined to match the Type of the Integrator that will receive the Discrete Change. Hence, although the Value itself is a vector (since it represents the values being pushed into the first row of the matrix), the Discrete Change element must be defined as a matrix (as it will be an input to a matrix Integrator).