The optimization algorithm can be controlled via the Precision setting in the Define Optimization Settings tab:
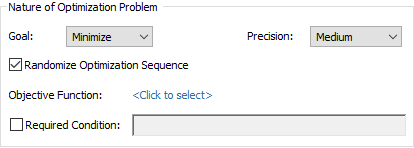
You can set the Precision to Maximum, High, Medium or Low (the default setting is Medium). The precision setting has two effects:
- it determines the number of valid points used to generate the initial complex of solutions; and
- it determines the convergence criterion GoldSim uses to decide whether or not it has obtained an "optimal" solution.
Box's complex method begins by developing an initial "complex," which is a set of valid solutions that meet all of the requirements specified by the user. This complex contains twice as many valid solutions as the number of optimization variables. Once the initial complex has been developed, the algorithm searches the solution space iteratively, replacing the least optimal members of the complex with more optimal ones until the solution converges or GoldSim determines that convergence cannot be achieved (in which case a warning message will be displayed).
The way in which the initial complex is generated depends on the Precision specified by the user:
- For Low Precision, GoldSim generates only the minimum number of valid solutions required to create the complex (i.e., two times the number of optimization variables).
- For Medium Precision, GoldSim generates twice as many valid solutions as it needs (i.e., it generates 4N valid solutions, where N is the number of optimization variables). It then uses the 2N most optimal solutions to form the initial complex.
- For High or Maximum Precision, GoldSim generates five times as many valid solutions as it needs (i.e., it generates 10N valid solutions, where N is the number of optimization variables). It then uses the 2N most optimal solutions to form the initial complex.
Hence, the higher the Precision setting, the better the initial complex spans the variable space (and the higher the likelihood that a global optimum, rather than a local optimum, will be found).
GoldSim determines whether or not it has achieved an optimal solution by comparing the range of objective function values in the current complex with the range of objective function values in the initial complex. The convergence criterion is also determined by the Precision specified by the user:
- For Low Precision, convergence requires the range in objective function values to be less than 0.01 of the initial range or 100 solutions have been tried.
- For Medium Precision, convergence requires the range in objective function values to be less than 0.001 of the initial range or 1000 solutions have been tried.
- For High Precision, convergence requires the range in objective function values to be less than 0.00001 of the initial range or 1E4 solutions have been tried.
- For Maximum Precision, the optimizer will continue until it can no longer improve the result, or 1E6 solutions have been tried.
In some cases, the optimization may not be able to converge within the allowed number of iterations. In this case, GoldSim will display a warning message.
The Randomize Optimization Sequence checkbox (which is checked by default), can be used to ensure that the initial complex is randomized every time it is created. This can be used to help ensure that GoldSim finds a global optimum by running the optimization more than once.
Learn more
- Defining the Optimization Settings
- Finding a Global Optimum in Complex Models with Multiple Optima
- Optimizing a Probabilistic Model
- Overview of Optimization
- Running the Optimization
- Saving Optimization Settings and Results
- Setting the Optimization Precision
- Specifying the Objective Function and Constraints
- Specifying the Optimization Variables
- Understanding Optimization Warning Messages