Proportional Controllers tend to work well if the expected uncontrolled inflows and outflows do not have a significant trend or pattern (such that a constant Bias can be easily specified to match them). For example, if you were defining an Outflow Controller (to compensate for a noisy inflow) and that inflow varied around some constant mean value (or was relatively steady but had short-term fluctuations), specifying the Bias as that mean inflow value would result in a Controller that worked reasonably well.
To illustrate this, consider the following example. In this model, there is a “noisy” inflow of water to a pond that changes daily (with a mean of 50 m3/day), and the Proportional Controller is an Outflow Controller. The goal is to approach and then maintain the volume near a target of 3000 m3 (the initial volume is 3030 m3):
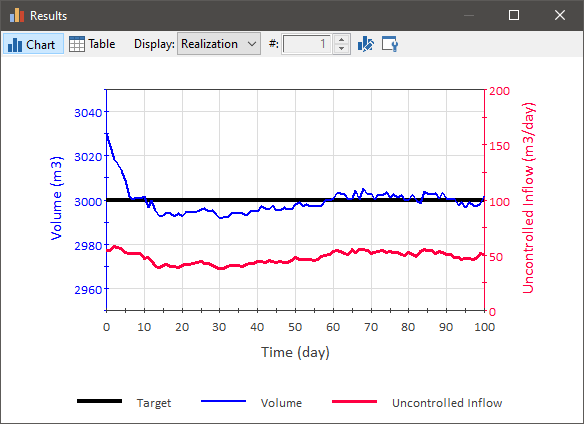
In this model, the timestep A discrete interval of time used in dynamic simulations. is 1 day, the Bias is set to 50 m3/day, the Proportional Gain is set to 1.5 day-1, and the Flow Capacity is set to 60 m3/day.
Does the timestep affect the performance of the Controller? Conceptually, a Controller is something that is being updated “continuously”. Of course, in a simulation model The implementation of a mathematical model of a system within a specific computational tool (or set of tools)., things are only updated on timesteps. So the timestep does indeed have an impact. Here is the same model as shown above with a 0.1 day timestep (instead of 1 day):
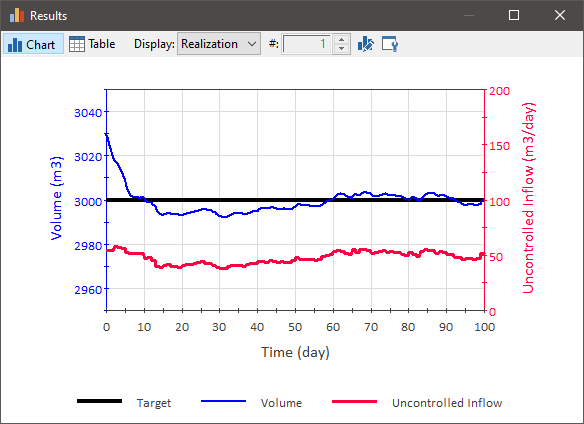
As can be seen, the process variable changes in a smoother manner (since the outflow is updated more frequently), although the general behavior is the same.
Note: Recall that in this example, the we are simulating an Outflow Controller (we are only controlling outflows). If this system had the ability to also have controlled inflows (and hence better performance when the value dropped below the target), you would simulate that by having two Controllers: and Inflow Controller and an Outflow Controller. Such a system would be able to better track the target.
While Proportional Controllers (with constant Bias and Gain) perform well if the expected uncontrolled inflows and outflows do not follow a trend or pattern (such that the Bias can be easily specified as a constant value), if the uncontrolled inflows and outflows follow a trend or pattern, Proportional Controllers (with a constant Bias and Gain) would result in poor performance. To illustrate this, consider an example where instead of the uncontrolled inflow having a constant mean, it steadily increases (in this model the Bias is 40 m3/day, the Proportional Gain is 1 day-1, and the Flow Capacity is essentially unlimited - 1000 m3/day):
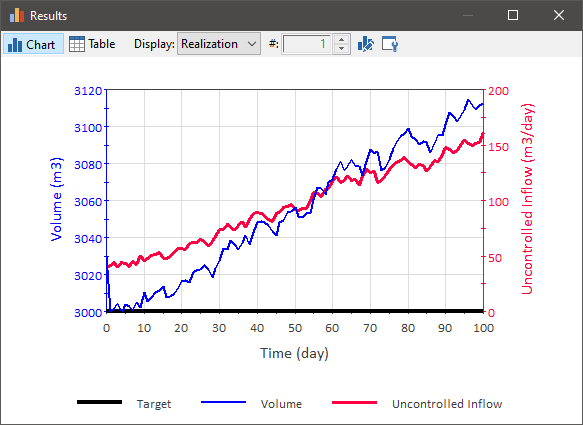
As can be seen, the Proportional Controller is unable to adjust the process variable back toward the target in this case (increasing the Proportional Gain in order to attempt to do so would better track the target, but would result in large oscillations around the target). In order to successfully use a Proportional Controller in this case it would be necessary to take the extra step of defining the Bias as being time variable in order for the Controller to perform well.
An example model which illustrates the basic use of the Proportional Controller (Proportional.gsm), in particular, the cases discussed in this