In many engineered (and some social and organizational) systems, there is active feedback control designed directly into the system to make it behave in a specified manner. That is, the system includes a feedback loop that is used to control behavior.
A thermostat is the classic example of this (the heating and/or cooling rate is adjusted based on the current temperature). Another example might be a pond (the pumping rate to and from the pond is adjusted based on the water level).
The goal of a feedback control system is generally to control the value of a state variable in the system (typically represented by a Reservoir or a Pool in GoldSim) by actively adjusting additions and withdrawals to that variable so that it is maintained at or around a target value (e.g., the set temperature value on a thermostat).
In the case of the thermostat, the state variable is the amount of heat in the house (quantified via the temperature) and the additions are withdrawals are associated with turning on/off the heat or air conditioning. For a pond, the state variable is the amount of water in the pond (which could be quantified via the water level) and the additions are withdrawals are associated with turning on/off pumps that remove (or perhaps add) water.
If you are going to model such systems, you need to understand how to properly represent these controlling feedback loops in a realistic way. In particular, it is quite common for novice (and even some experienced) modelers to represent such systems in such a way that the model behaves quite poorly (e.g., oscillates unrealistically).
One of the best ways to avoid the potential for unrealistic oscillatory behavior (and to realistically represent how the system would be managed in the actual system) is use what is referred to as a “deadband” or a target range within which the system is controlled. This is actually how a thermostat typically works (e.g., “turn the heat on when the temperature is 68 degrees and turn it off when it reaches 70 degrees”). You could implement this in GoldSim using a Status element.
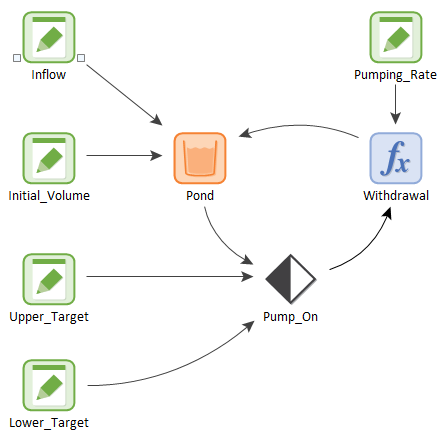
To illustrate this, let’s consider the example pictured below (you can find this example in Reservoir.gsm in the General Examples/Stocks folder of your GoldSim directory, accessed by selecting File | Open Example... from the main menu):

 Note: A similar example using a Pool
instead of a Reservoir can be found in Pool.gsm in the General Examples/Stocks
folder of your GoldSim directory, accessed by selecting File | Open
Example... from the main menu.
Note: A similar example using a Pool
instead of a Reservoir can be found in Pool.gsm in the General Examples/Stocks
folder of your GoldSim directory, accessed by selecting File | Open
Example... from the main menu.
In this simple model, water flows into a pond at a constant rate (100 m3/day), and we wish to actively control the volume of water in the pond, maintaining the volume between a lower target or 290 m3 and and upper target of 310 m3 (the “deadband”). We do this by turning a pump (that removes water from the pond) on and off in a specified manner. The pump, when on, pumps at a rate of 200 m3/day.
The Status element is used to determine if the pump is on or off. Its triggers are defined as follows:
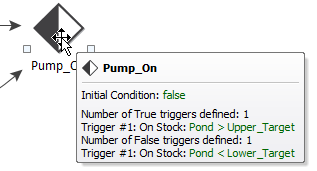
 Note: The triggers are defined as
“On Stock” triggers, which force an unscheduled update at the point the condition is met,
resulting in more accurate behavior. Using “On True” triggers would be less
accurate (as unscheduled updates would not be created, and the trigger would
not be pulled until the next scheduled update).
Note: The triggers are defined as
“On Stock” triggers, which force an unscheduled update at the point the condition is met,
resulting in more accurate behavior. Using “On True” triggers would be less
accurate (as unscheduled updates would not be created, and the trigger would
not be pulled until the next scheduled update).
The Withdrawal from the pond is then defined as follows:
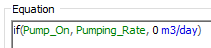
That is, when the pond volume is greater than the upper target volume, the pump is turned on. When it is below the lower target volume, it is turned off. Note that the Pumping_Rate is larger than the Inflow, so when the pump is turned on, the volume in the pond is reduced. The essentially creates a feedback loop between the pond volume and the withdrawal – it is an active feedback control system that is analogous to those common in many engineered systems.
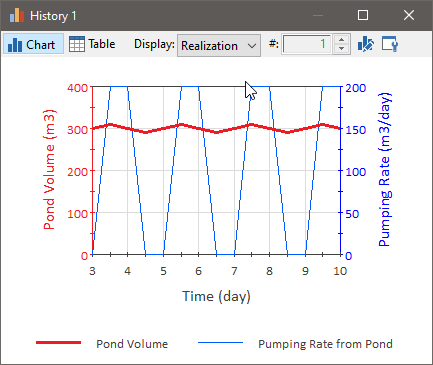
The pond volume behaves as follows, slowly moving between the two targets:
Learn more about:
Understanding State Variables in GoldSim
Avoiding Oscillatory Behavior When Using Reservoirs