Using an Integrator to Compute Moving Averages

In some cases you may want to represent a moving average in your model. For example, at any given time, you might want to know what the average value was over the previous 30 days.

You can use an Integrator to compute a moving average of the Rate of Change input.

A moving average is a uniformly-weighted average of the Rate of Change over a specified averaging time (ATime). It is calculated as the change in the value of the Integrator over the averaging time divided by the averaging time:

Note: To account for elapsed times that are less than the averaging time, the actual averaging time used is the minimum of the elapsed time and the specified averaging time. The value of the moving average at elapsed time = 0 is equal to the initial value of the Rate of Change.

GoldSim provides an option to compute up to three different moving averages. To activate it, you must press the More button to expand the dialog:

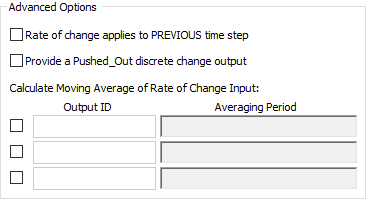
By checking a box, you can specify the name of the moving average output and define the Averaging Period. If you specify multiple moving average outputs, they must have unique names. The Output IDs follow the same naming conventions as element names. The Averaging Periodmust have units of time, and must be a number or a link from a static variable (e.g., a constant Data element An input element intended to represent constant inputs in a model. or some other output that does not change with time).

Discrete changes (applied in the Discrete Change field) will affect the moving average outputs. In particular, any discrete changes that are applied to the Integrator will affect the moving average as if they were distributed uniformly over the preceding timestep A discrete interval of time used in dynamic simulations. (i.e., from the previous update of the element to the update where the discrete change was applied.

Note: The moving average outputs have the same dimensions An output attribute for an element that defines the dimensionality (in terms of Length, Time and other fundamental dimensions) of the output. as the Rate of Change input (not the dimensions defined by the Display Units The units (e.g., m, g, $/day) in which an output is displayed within GoldSim. for the Integrator itself). For example, if the variable you are interested in computing a moving average for has dimensions of volume/time, then the Integrator would need to have dimensions of volume. Similarly, if the variable you are interested in computing a moving average for has dimensions of mass, then the Integrator would need to have dimensions of mass-time.

Note: The Display Units for the moving average outputs are the Display Units for the element divided by the Time Display Units (specified in the Simulation Settings dialog). If this results in unusual Display Units, you can simply route the output into an Expression with adjusted Display Units.