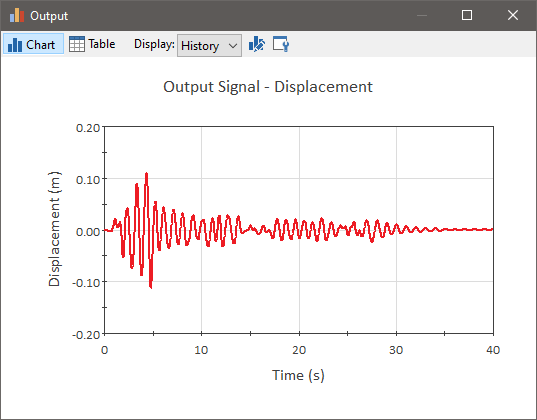
This example shows how a Convolution element An element that solves a convolution integral. can be used to simulate how a structure responds to an earthquake. The input signal is an accelerogram (a time history of ground accelerations). The output signal is the displacement of a building (illustrating how the building oscillates from side to side in response to the earthquake).
The input signal (the accelerogram) is taken from an actual earthquake in Southern California in 1940 (the El Centro earthquake):
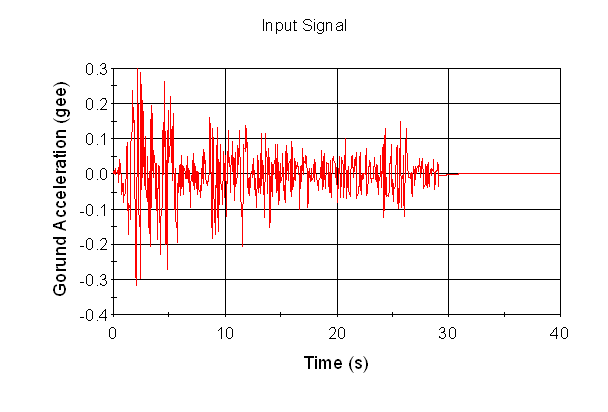
As can be seen, the earthquake lasted about 30 seconds.
For simplicity, the building is treated as a damped spring. The transfer function under such an assumption is represented by the following equation:
where n is the coefficient of decay (in radians/sec), and Wd is the damped frequency (in radians/sec). A plot of this transfer function looks like this:
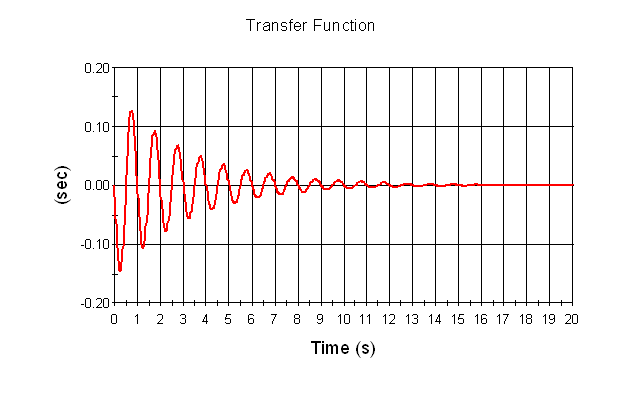
The transfer function represents the ratio of a displacement response to a "pulse" of ground velocity, and has dimensions An output attribute for an element that defines the dimensionality (in terms of Length, Time and other fundamental dimensions) of the output. of time.
This curve indicates that once excited by an impulse, the building oscillates with the oscillations dying out within about 15 seconds.
The output signal will have dimensions of length:
Output = Transfer Function * Input Signal * time
Output = sec * m/sec2 * sec = m
That is, the output represents the displacement of the building in response to the earthquake: