Defining Initial and/or Boundary Conditions for a Cell

There are four ways by which species The chemical (or non-chemical, such as bacterial or viral) constituents that are stored and transported through an environmental system in a contaminant transport model. In GoldSim, the Species element defines all of the contaminant species being simulated (and their properties). mass can enter a Cell:

1. By defining an initial condition and/or a boundary condition for the Cell;
2. By defining discrete changes to the inventory in a Cell;
3. Through a mass flux link An interconnnection between two transport pathways that defines the rate at which species move between the pathways. from another pathway to the Cell; and/or
4. By associating the Cell with a Source.

Below we discuss the first item, defining an initial and/or boundary condition for a Cell.

An initial condition/boundary condition for a Cell is specified within the "Cell Inventory" section of the dialog. The first field in this section provides four options:

• Initial Inventory. This is the default, and represents the initial inventory of each species. This field only accepts vectors by species with dimensions An output attribute for an element that defines the dimensionality (in terms of Length, Time and other fundamental dimensions) of the output. of mass. Moreover, this input cannot be specified as a function of time (if it is, GoldSim will display a fatal error when you try to run the model).
• Cumulative Input. This option provides a mechanism for simultaneously specifying an initial condition and a rate of mass addition (that may change with time). This field only accepts vectors by species with dimensions of mass. It represents the cumulative amount of mass of each species added to the Cell at a given time. Hence, if it is constant, it represents an initial condition. If it increases with time, its rate of change represents a specified rate of addition. Correct use of the "Cumulative Input" is summarized in the table below:

To specify this:	Enter the following into the "Cumulative Input" field:
An initial condition	A constant vector A one-dimensional array. with dimensions of mass (in this case, however, it would be more transparent to use the "Initial Inventory" option).
An initial condition and a constant rate of addition	An expression such as: Initial + Rate * Etime, where Initial is a constant vector (with dimensions of mass) and Rate is a constant vector (with dimensions of mass/time).
An initial condition and a time-variable rate of addition	The output of a Pool A stock element that integrates and conserves flows of materials. A Pool is a more powerful version of a Reservoir (it has additional features to more easily accommodate multiple inflows and outflows)., Reservoir A stock element that integrates and conserves flows of materials. or Integrator element An stock element that integrates rates. (with output dimensions of mass) with a specified Initial Value and (time-variable) Rate of Change.

Warning: The Cumulative Input must stay constant or increase with elapsed time. That is, you cannot remove mass from a Cell using the Cumulative Input field. If the value ever begins to decrease with time, a fatal error occurs.

• Input Rate. The third Cell Inventory option is used to specify a rate of mass addition (that may change with time). This field only accepts vectors by species with dimensions of mass/time. It represents the rate at which mass of each species is added to the Cell over the next timestep A discrete interval of time used in dynamic simulations..
• Defined Concentration. The fourth Cell Inventory option is used to specify a concentration boundary condition. This field only accepts vectors by species with dimensions of mass/volume. This option fixes the concentration of each species in the first fluid listed in the Media Materials (such as water, sand, clay, air) that constitute (are contained within) transport pathways. GoldSim provides two types of elements for defining media: Fluids and Solids. list at the defined level. The concentration represents the dissolved concentration. (If the Cell contains suspended solids, the total concentration could be higher.) The Defined Concentration can be specified as a function of time.

Note: One way to easily enter a vector of data into an input field without having to create a separate element is to use GoldSim's vector constructor function. For example, entering "vector(1g)" into the Cumulative Input field results in an initial condition of 1 g of each species being present in the Cell.

Note: A Defined Concentration boundary condition does not use the specified volume of the first fluid to compute a concentration (it simply applies a specified concentration). However, you should still specify a volume (e.g., 1 m³). If you specify a zero volume, it will generate a warning message when you run the model.

Warning: If you select a Defined Concentration boundary condition and leave the input field blank, GoldSim will assume a zero concentration for all species.

Warning: A Defined Concentration boundary condition can act as both a source and a sink. As a simple example, specifying a concentration of zero would turn the Cell into a sink for mass. Not only would diffusive gradients be toward the Cell, but any mass entering the Cell (by any mechanism) would be removed from the system (in order to maintain a zero concentration).

Warning: Solubility limits are not applied in Cells with a Defined Concentration. If the Defined Concentration for a species is above the solubility limit, the solubility limit is ignored, the Defined Concentration is applied, and a warning is written to the Run Log Text that is stored with a GoldSim model once it has been run. It contains basic information regarding the simulation, and any warning or error messages that were generated..

Although the Input Rate and Cumulative Input options provide a quick and convenient way to enter mass input rates, if mass input rates into a Cell are changing with time (e.g., because the inflow concentration is changing), a slightly more accurate way (both numerically and conceptually) to specify such a boundary condition is to create a second Cell that is defined using a Defined Concentration.

As an example, consider a case in which you have a boundary condition with a constant inflow rate (Flow_Rate) and a time-varying Inflow_Concentration. There is also an Initial_Concentration in the Cell, which has a Constant_Volume and constant outflow rate (equal to the inflow rate). You could model this in two ways, as illustrated in the example below:

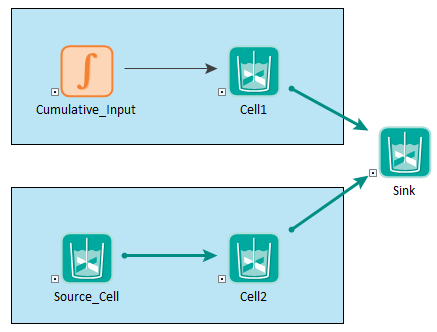
The example in the top uses the Cumulative Input option for the "Cell Inventory" in Cell1:

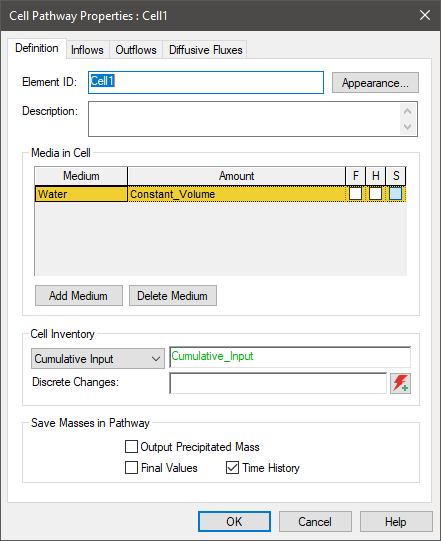
The Cumulative_Input Integrator element is defined as follows (with an initial mass and a mass input rate):

The example on the bottom defines a "Source_Cell" that looks like this:

The volume is set to an arbitrarily small number (it is not used to compute concentrations since the concentration is fixed). A Defined Concentration is specified for this Source_Cell that will flow into Cell2. That is, the Source_Cell has an outflow to Cell2:

Cell2 looks like this:

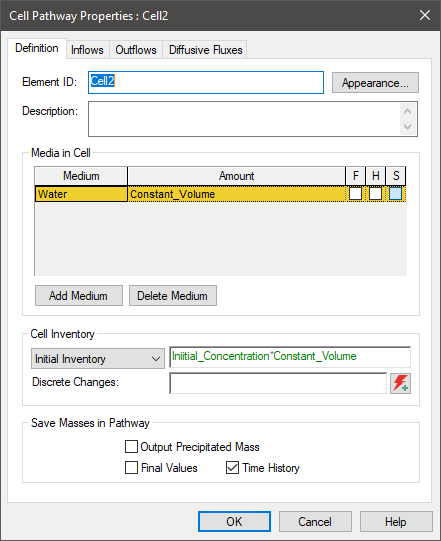
It has an Initial Inventory, as well as an inflow from the Source_Cell.

If we run this model (for 100 days with a 5 day timestep) and compare the results for these two different approaches to representing the boundary condition (in terms of mass in Cell1 and Cell2), they look like this:

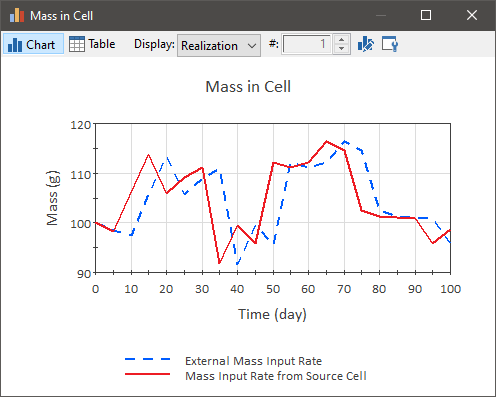
What we see is that the mass that is input "externally" (using the Cumulative Input) lags by one timestep. This is because in this approach (or in the absence of an initial condition, using an Input Rate), due to the way the external boundary condition must be applied when solving the pathway equations, a one timestep lag is introduced. Hence, the second approach is a more accurate representation (although for a small timestep, the differences would likely be insignificant). Conceptually, however, this is a bit more accurate way to represent the boundary condition (since the boundary condition is actually treated as part of the pathway network).