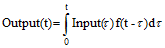
In the absence of dispersion and assuming a constant Delay Time, the output of an Information Delay is simply computed as follows:
Output(t) = Input(t - Delay Time)
If the signal is dispersed (or the Delay Time is variable), the solution involves a convolution integral of the form:
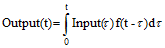
f(t) is the gamma probability distribution, which is equivalent to (and a generalization of) the Erlang distribution that is frequently used in simulation models. f(t) represents the probability density of the time of “release” from the delay of an input at time 0:
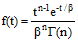
where:
n is the Erlang value (specified by the user);
β = D/n;
D is the mean delay time; and
Г is the gamma function (not the Gamma distribution).
The Erlang distribution is equivalent to the distribution of passage times through a cascaded series of n mixing cells, each of which has a mean residence time of D/n. The gamma distribution represents the time until the occurrence of n sequential Poisson-process events, where each event’s random time is represented by an exponential distribution with mean D/n.
The gamma distribution is a generalized version of the Erlang distribution, and does not require n to be an integer. Note that for n=1, the distribution is exponential, and for increasing values of n it becomes less skewed, approaching normality for large n.
The standard deviation of the gamma probability distribution is equal to D/√n. The degree of dispersion for an Information Delay can be specified in terms of either n or the standard deviation.
GoldSim actually solves the convolution integral by first carrying out a transformation of the time axis. This allows for accurate representation of variable Delay Times.
Learn more about: