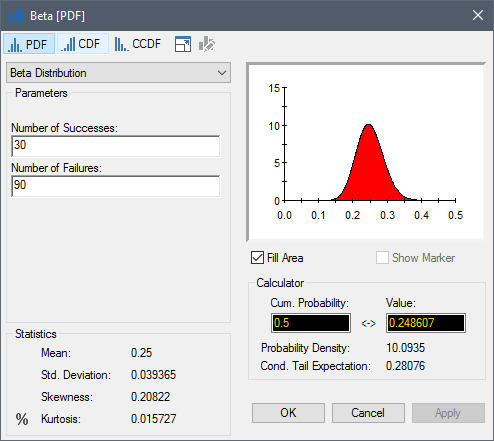
The Beta distribution is a continuous distribution used to represent the uncertainty in the probability of occurrence of an event given some data regarding observations of the event occurrence in previous experiments. As such, the Beta distribution represents the probability distribution of a frequency, and therefore always ranges between 0 and 1.
It is defined by specifying results of an experiment or a number of trials (e.g., a coin flip) in terms of Number of Successes and Number of Failures:
Both inputs must be positive values. The displayed distribution represents the underlying probability of a Success. For example, in the screen shown above, if we define Success as heads on a coin flip, and Failure as tails, the distribution represents the uncertainty in the probability of obtaining heads on the next flip of the coin. If the number of trials is small, the uncertainty is high. As the number of trials increases, the uncertainty in the outcome decreases (and in the example of a coin flip, if the coin is unbiased, the probability of heads would collapse to 0.5).
Note:
The Beta distribution must always be dimensionless, as it represents a frequency
(otherwise GoldSim will display an error). However, GoldSim also provides a
generalized form of the Beta that allows you to specify a distribution’s
dimensions (e.g., time). Such a distribution is defined in a different way
(using a mean, standard deviation, minimum and maximum). The Generalized
Beta distribution therefore provides a
flexible way to specify a probability distribution over a particular
range.
Learn more about: