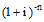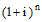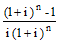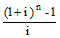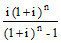Financial Functions: Simple Compounding

The first five financial functions are simple compounding functions that account for the time value of money and convert between present value, future value and annuities. These are dimensionless functions that act as multiplying factors on a currency amount (e.g., $) or currency rate (e.g., $/yr).

In these functions the first argument (int. rate) is the fractional interest per period (expressed as either a fraction or a percentage), and the second argument (#periods) is the number of periods:

Function	Description	Definition
ftop(int. rate, #periods)	Factor that when multiplied by a future amount returns the present value of that future amount.
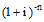
ptof(int. rate, #periods)	Factor that when multiplied by a present amount returns the future value of that present amount.
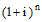
atop(int. rate, #periods)	Factor that when multiplied by an annuity amount returns the present value of that annuity.
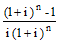
atof(int. rate, #periods)	Factor that when multiplied by an annuity amount returns the future value of that annuity.
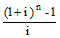
ptoa(int. rate, #periods)	Factor that when multiplied by a present amount returns the annuity of that present amount.

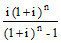
int. rate (i): Must be greater than zero. Can be a scalar or an array
#periods (n): Must be a positive scalar.

These functions assume discrete compounding. That is, the functions assume compounding once per period.

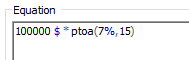
Since #periods represents the number of periods in these functions, it must be a unitless value. For example, in order to compute the annuity value (the annual payment amount) for a 15 year loan of $100,000 with an interest rate of 7% per year (compounded annually), you would write the following in an expression: