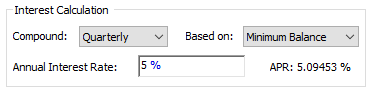
The accounts and funds that you simulate using a Fund element generally will accumulate (or charge) interest that is compounded in a particular manner. The "Interest Calculation" portion of the dialog is used to specify this information:
Several options are available in the Compound drop-list to determine how interest is compounded. In all cases (except when "None" is specified), you must define an Annual Interest Rate. GoldSim displays the expected value of the APR (Annual Percentage Rate) to the right of the interest rate.
The actual interest rate that GoldSim uses for the calculation, as well as how the APR is calculated is summarized in the table below (where "Rate" represents the nominal interest rate specified in the Annual Interest Rate field). The Annual Interest Rate can be entered as a fraction or a percentage (with the % symbol).
Note that by definition, for all compounding methods except annual, the APR is actually higher than the Annual Interest Rate.
|
Compounding Option |
Interest Rate Used |
APR |
|
Continuous |
Rate |
eRate - 1 |
|
Monthly |
Rate / 12 each month |
(1 + Rate/12)12 - 1 |
|
Quarterly |
Rate / 4 each quarter |
(1 + Rate/4)4 - 1 |
|
Annual |
Rate each year |
Rate |
Note:
Daily compounding can be simulated by selecting Continuous, and specifying an
Annual Interest Rate (Rate) as
follows:
Rate = pc2cc(DailyRate, 365)
where DailyRate is the nominal annual
interest rate (assuming daily compounding) you are trying to compute. The
function pc2cc is a built-in financial function that converts a periodic rate to
an equivalent continuous rate.
You must specify what the Interest is based on in the Based on field. There are three options: "Minimum Balance", "Average Balance", or "Maximum Balance". This field is grayed out if Continuous compounding is selected, as in this case interest is always based on the current value.
For monthly, quarterly and annual compounding, the interest is applied as a lump sum at the end of each compounding period. For continuous compounding, the interest is applied at every model timestep:
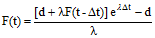
where:
F(t) is the value of the fund at time t;
Δt is the timestep length;
F(t-Δt) is the value of the fund at time t – Δt (i.e., the previous timestep);
λ is the specified nominal annual interest rate (at time t); and
d is the net amount deposited over the timestep.
The following should be noted regarding how interest is calculated in a Fund element:
•For monthly, quarterly, and annual compounding, GoldSim automatically inserts a new timestep at the appropriate time in order to implement the compounding. For elapsed time simulations, GoldSim inserts a timestep once every 365.25/12 days for monthly compounding, once every 365.25/4 days for quarterly compounding, and once every 365.25 days for annual compounding. For date-time simulations, a timestep is added every month, every 3 months or every year (always on the same day of the month as the simulation started on).
Warning: Inserting the necessary timesteps
for monthly or quarterly compounding adds some overheard to the model. If
you don't need precision in the timing of interest payments, you can use the
"continuous compounding" option and convert you quarterly or monthly rate to an
equivalent continuous rate using the pctocc function. For example, Monthly
compounding can be simulated by selecting Continuous, and specifying an
Annual Interest Rate (Rate) as
follows:
Rate = pc2cc(MonthlyRate, 12)
where MonthlyRate is the nominal annual
interest rate (assuming monthly compounding) you are trying to compute. The
function pc2cc is a built-in financial function that converts a periodic rate to
an equivalent continuous rate.
•Discrete deposits or withdrawals received at the end of a compounding period are not taken into account for the purposes of calculating the minimum, maximum or average balance for the period.
•If the Fund value is negative, the interest rate is still applied, but in the negative direction.
Learn more about:
Financial Functions: Continuous/Periodic Compounding Conversions