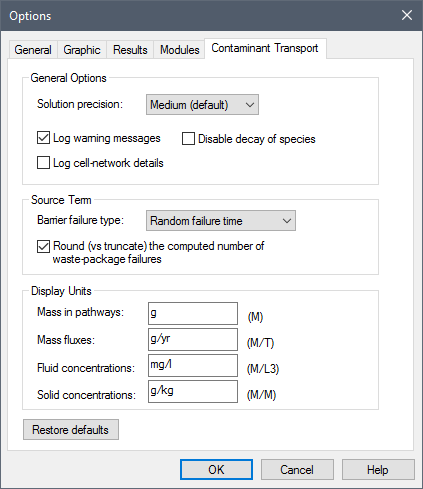
There is one aspect of the solution algorithm that you may need modify in order to increase the accuracy of simulations using Pipes. This feature is accessed via the Contaminant Transport tab in the Options dialog (accessed from the main menu items Model | Options...):
GoldSim uses a particular algorithm (the de Hoog algorithm)
to carry out the Laplace transform A method for solving certain types of differential equations that involves transforming the equations into an algebraic form that can be readily solved, and then using an inverse transform to retrieve the solutions of the original problem.
calculations. This algorithm includes a parameter which controls the
number of terms used in an approximation within the solution. The number of
terms used is determined by the Solution precision field in the Options
dialog (note that this field also controls the precision of the Cell pathway A transport pathway element that is mathematically equivalent to a finite difference node. Cells are commonly applied to simulate discrete compartments in an environmental system (such as ponds, lakes, shallow soil compartments, or the atmosphere). algorithm). There are three
possible choices for the solution precision (Low, Medium, High). If Medium
is selected (the default), GoldSim uses 15 terms in the Laplace transform
solution. If Low is selected, it uses 5; if High is selected, it uses
25. You only need be concerned with this value if you are trying to
simulate Pipes with very low dispersivity values. In such a case, you may need
to select High precision (i.e., 25 terms) in order to reduce oscillations in
your computed fluxes. The solution algorithm for Pipes is discussed in
detail in
- Advective-Dispersive Transport in Pipes
- Comparing Pipes and Aquifers
- Computing Pipe and Aquifer Pathway Concentrations Accounting for Transverse Dispersion
- Controlling the Pipe Solution Algorithm
- Defining a Sorptive Coating Material for a Pipe
- Defining Basic Pipe Properties
- Features and Capabilities of Pipes
- Flux Links to/from Pipes
- Pipe Pathway Outputs
- Saving Results for a Pipe
- Simulating Storage Zones in a Pipe
- Simulating Suspended Solids in a Pipe
- Simulating Time-Variable Pipe Properties
- Summary of Limitations on the Use of Pipe Pathways
- Viewing a Pipe in the Browser